שבוע 3
אם פספסתם משהו או סתם לא זוכרים, לחצו כאן כדי לעבור לשבוע 2.
הערה – אם אתם גולשים מהנייד, חלק מהנוסחאות עלולות "להימרח" לצדדים. סובבו את המכשיר לרוחב אם זה קורה.
השבוע יהיה קצת יותר ארוך מהשבועות הקודמים. תהיו חזקים (כאילו יש לכם מה לעשות, אתם בסגר).
סיווג (Classification)
נעבור לתחום הסיווג, שההבדל מרגרסיה הוא שהתוצאות שאנו רוצים לחזות מסווגות למספר מוגבל של אפשרויות, כגון זיהוי ספאם באימייל (ספאם או לא ספאם), העברות בנקאיות באינטרנט (אמיתי או מזויף) וכולי.
ערכי $y$ יכולים להיות כל דבר, אבל באופן טבעי לרוב נעבוד כשהפלטים האפשריים של y יהיו 0 או 1 (אין או יש), ונמשיך הלאה עם 2,3 וכולי אם זו בעיית סיווג מרובה. כרגע נעבוד על בעיית סיווג בינארית (רק 2 אפשרויות לפלט), ולאחר מכן נרחיב למקרה הכללי.
הסיבה שרגרסיה ליניארית לרוב אינה מתאימה לבעיות סיווג, היא שהפלט שהיא מחזירה נע על טווח ערכים הרבה יותר רחב מהערכים שדרושים לנו. ובעוד שיטת הרגרסיה מתייחסת למרחק היחסי בין כל התצפיות שלנו (ויכולה בעקבות מקרי קצה להיות קרובה יותר לקבוצה אחת מאשר לאחרת) – בעיות סיווג מחפשות למעשה רק איזשהו "קו מפריד" בין קבוצה של תצפיות לקבוצה אחרת. אנחנו מצפים לקבל החלטה, ולא ערך.
רגרסיה לוגיסטית (Logistic Regrssion)
אז ככה – מטרתנו היא לייצר היפותזה $h(x)$, כך ש $0<h(x)<1$ (כל התחזיות נופלות בן 0 ל-1). איך עושים את זה? נסביר באמצעות קצת מתמטיקה:
פונקציית הסיגמואיד, או "הפונקציה הלוגיסטית", היא פונקציה מתמטית מוכרת (תלוי למי כמובן) בעלת צורה בסגנון של האות S, כשבשאיפה למינוס אינסוף היא שואפת ל0, ובשאיפה לאינסוף היא שואפת ל1:
$$g(x) = \frac{1}{1+e^{-x}}$$
המקרה הכללי שלה נראה בד"כ ככה:
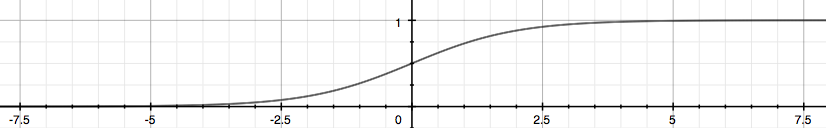
ויש לה שימושים רבים כמעט בכל תחום, בין היתר בסטטיסטיקה, שקשורה לתחום שאנו עוסקים בו כעת (באמת המון שימושים, אפשר לקרוא עליה בגוגל).
כעת, במקום $x$, נכניס את ה$h(x)$ הקודמת שלנו, ונקבל למעשה פונקציה שמעבירה כל ערך שקיבלנו אל תחום מספרים בין 0 ל1, שבמילים אחרות ייצג בשבילנו את ההסתברות של תצפית מסוימת להיות בקבוצה הראשונה או השנייה (0 או 1).נציב את $h(x)$ שלנו, והפונקציה תיראה ככה:
$$g(h_\theta(x)) = \frac{1}{1+e^{-h_\theta(x)}} = \frac{1}{1+e^{-\theta^{T}x}}$$
עוד מושג חשוב בתחום הוא גבול ההחלטה (decision boundary), שהוא למעשה הקו שמפריד בין קבוצה אחת לשנייה. הוא נוצר בהתאם לערכי $\theta$ שמצאנו, ויכול לבוא בשלל צורות (מקו ישר ופשוט, עד לעיגולים וצורות מיוחדות). מצד אחד שלו כל התצפיות שייכות לקבוצה אחת, ומהצד שני לקבוצה אחרת.
פונקציית עלות (Cost Function)
אם נשתמש בפונקציית העלות הקודמת שלנו גם לרגרסיה לוגיסטית, נקבל פונקציה שאינה קמורה (convex). שבעברית זה אומר שתהיה מין צורה "גלית" כזאת לפונקציה עם מלא נקודות מינימום מקומיות, מה שימנע מאיתנו להגיע למינימום המוחלט. במקום זאת, נשתמש בפונקציה הבאה:
$$J(\theta) = \frac 1m \sum_{i=1}^m Cost(h_\theta(x^{(i)}),y^{(i)})$$
כש-
$$Cost(h_\theta(x),y) = -\log(h_\theta(x)) \quad y =1 םא $$
$$Cost(h_\theta(x),y) = -\log(1 – h_\theta(x)) \quad y =0 םא $$
כשהפונקציה $Cost(h(x),y)$ שווה לאותו חלק שהיה בתוך הסיגמא של פונקציית העלות הקודמת, משמע $Cost(h(x),y) =\frac 12 (h(x)-y)^2$ (את ה$\frac 1m$ אנחנו משאירים בחוץ).
עכשיו, קלטו את הקסם. בגלל תכונות הלוגריתם, נקבל בדיוק את הפונקציה הקמורה שרצינו: כש$y=1$, הפונקציה תהיה $-log(h_\theta(x))$, מה שאומר שכ$h(x)=1$, הפונקציה תשאף ל0, וכש$h(x)=0$ הפונקציה תשאף לאינסוף.
והפוך במקרה ש$y=0$: כש$h(x)=1$, הפונקציה תשאף לאינסוף, ולעומת זאת, כש$h(x)=0$, הפונקציה תשאף ל0.
אם לסכם בעברית את כל האותיות האלו – זה אומר משהו מאוד פשוט: ככל שההיפותזה שלנו – $h(x)$ – יותר קרובה לתוצאה האמיתית – $y$ – אז הטעות שלנו – $J(\theta)$ – קטנה יותר, וכן להיפך.
אם זה מבלבל אתכם, נסו להסתכל שוב על שני המקרים של הפונקציה ולהציב ערכים ל$h(x)$ ולראות מה יצא.
טוב, אז מצאנו את הפונקציה שלנו, אבל איך עכשיו נארגן לה מינימום כשזה בתכלס שתי פונקציות? למזלנו, בגלל שy הוא תמיד 0 או 1, נוכל להשתמש בטריק יפה ופשוט לכתוב אותן בשורה אחת, ממש ככה:
$$ Cost(h(x),y) = -y\,\log(h_\theta(x)) –(1-y)\,\log(1 – h_\theta(x))$$
וכן, זה עובד – תבדקו בעצמכם. (מה אני מורה למתמטיקה? איזה עם קשה עורף בחיי)
אלגוריתם מורד הגרדיאנט של רגרסיה לוגיסטית עדיין ייראה בדיוק אותו דבר כלפי חוץ, אבל חשוב לזכור שאנחנו משתמשים בפונקצית $h(x)$ שונה (עם כל הסיגמואיד וזה). וקטוריזציה של האלגוריתם תיראה כך:
$$\theta := \theta – \frac{\alpha}{m} X^T (g(X\theta) – \vec{y}) $$
קיימים אלגוריתמים יותר יעילים ממורד הגרדיאנט, שהם BFGS, ,L-BFGS וConjugate gradient. באופן כללי הם יותר מהירים ממורד הגרדיאנט ואין בהם צורך לבחור ידנית את קצב הלמידה, אך הם יותר מסובכים למימוש והבנה. למרות זאת, ניתן להשתמש באלגוריתמים אלו דרך ספריות של השפות השונות ולקבל תוצאות טובות. בכל מקרה, עדיין כדאי לבדוק אם הן מומשו טוב בספריה שאתם משתמשים בה.
באוקטב, נפעיל את האלגוריתמים האלו באופן הבא: נכתוב את פונקציית העלות שלנו שתחזיר את $J$ ואת הנגזרות לכל $\theta$:
עכשיו, נשתמש בפונקציה fminunc() כדי להריץ את האלגוריתם:
כשבoptions אנו מגדירים האם אנחנו מספקים נוסחא לגרדיאנט (on במקרה שלנו) ומספר איטרציות, מאתחלים את ערכי ה$\theta$ ושולחים את כל זה לפונקציה. @ מסמל מצביע, והערכים המוחזרים הם ערכי ה$\theta$ האופטימלים, ערך השגיאה האופטימלי (מינימום מוחלט) והאם האלגוריתם נעצר בהצלחה (לפי הסדר).
סיווג רב קבוצתי (Multiclass classification)
אחלה תרגום מושגים אני עושה פה.
נעבור לדבר על בעיות סיווג עם למעלה מ2 אפשרויות – לדוגמה, תיוק מיילים לתיקיות עבודה, לימודים, חברים ומשפחה, או בדיקת חום – גבוה, נמוך וממוצע.
אחת מהדרכים לגשת לבעיות כאלו היא בשיטת אחד-נגד-כולם (נקראת one-vs-all, או one-vs-rest), שאומרת את הרעיון הפשוט הבא (שמובן קצת מהשם של השיטה, בתכלס): בכל שלב, נבחר קבוצה אחת ונריץ עליה את אלגוריתם הרגרסיה הלוגיסטית מול כל התצפיות אחרות (כאילו הן כולן קבוצה אחת), ואת זה נעשה לכל קבוצה בנפרד. הדרך הזו היא בעצם "פירוק" של מספר רב של קבוצות לבעיה בינארית שאנחנו כבר מכירים. בכל פעם לוקחים קבוצה אחת ושמים כנגדה את כל הקבוצות האחרות.
בסופו של דבר, אם יש לנו n קבוצות – נקבל n היפתוזות וn גבולי החלטה. ברגע שתבוא תצפית חדשה, פשוט נחפש את ההיפתוזה $h(x)$ מביניהן שכשנציב את התצפית, היא תיתן עבורה את הערך המקסימלי – $\max(h_\theta^{i}(x))$ (האות i מייצגת את ההיפותזה מספר i).
רגולריזציה (Regularization)
האלגוריתמים שלמדנו עד עכשיו יכולים לפתור המון בעיות, אבל גם עלולים להיכנס לבעיה שנוהגים לקרוא לה "התאמת-יתר" (overfitting), כאשר הפונקציה שקיבלנו מתאימה מידי למידע הנתון (ובכך לא מתאימה למקרה הכללי), או התאמת חסר (underfitting) למקרה שהפונקציה שלנו לא מספיק מדויקת ביחס למידע שבידינו (ואז היא פשוט לא מספיק מדויקת למקרה הכללי).
בשני המקרים האלו אנחנו עלולים לגלות שתצפיות חדשות שנרצה להוסיף לא יקבלו ערך הגיוני, והפונקציה שלנו תהיה חסרת ערך. כדי לפתור בעיות כאלו לרוב יש שתי דרכים:
- מחיקה של מאפיינים – מה שיעזור בצמצום הבעיה והפונקציה, אך מצד שני יימחק לנו מידע שיכל לעזור לנו. אפשר למחוק ידנית או דרך אלגוריתם (יילמד בעתיד).
- רגולריזציה – באופן כללי: השארת כל המאפיינים, ובמקום זה הקטנת הערכים של $\theta$.
מה?
כן. הקטנת הערכים – והרעיון מאחורי זה הולך ככה: כשיש לנו מספר רב של פרמטרים, האלגוריתמים שלנו ינסו למצוא כמה שיותר דיוק לכל אחד מהמאפיינים ולכן נקבל $\theta$ שיתאימו "מידי" לדוגמות שלנו. אבל אם נגיד לאלגוריתם "להרגיע" ולהקטין כל פרמטר, נקבל גרסה פשוטה יותר של הפונקציה שלנו, שעדיין קולעת למקרה הכללי אבל לא מדויקת "על המילימטר" כדי לגרום לבעיה של התאמת יתר.
כשאנחנו בונים את האלגוריתם מטרתנו היא למצוא את הערך המינימלי של פונקציית העלות, לכן מעכשיו היא תיראה כך:
$$\min_\theta \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)} – y^{(i)})^2 + \lambda \sum_{j=1}^n \theta_j^2$$
כשהסיגמא בהתחלה זה הפונקציית עלות שלנו, והסיגמא שבסוף היא התוספת לצורך הרגולריזציה, והלמדא ($\lambda$) נקראת פרמטר הרגולריזציה. למדא גבוהה מידי תיתן התאמת חסר – כי היא תמחוק כמעט לגמרי את ה$\theta$, למדא נמוכה מידי לא תשפיע מספיק – ותשאיר את התאמת היתר.
הוספה של הרגולריזציה למורד הגרדיאנט של רגרסיה ליניארית, תהפוך כל איטרציה של האלגוריתם לחישוב הבא:
$ \theta_0 := \theta_0 – \alpha \frac {1}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) – y^{(i)}) \cdot x_0^{(i)} $
$ \theta_j := \theta_j – \alpha [\frac {1}{m} \sum_{i=1}^m (h_\theta(x^{(i)}) – y^{(i)}) \cdot x_j^{(i)} + \frac{\lambda}{m} \theta_j ] $
כאשר $j \in \{1,2…n\}$
אם נשים לב, הביטוי $\frac{\lambda}{m}$ ליד ה$\theta$ תמיד יהיה קטן מ1, כך שאינטואיטיבית אנחנו מבצעים בכל שלב את אותו אלגוריתם שהכרנו רק שהת'טות קטנות במעט בכל שלב.
הוספה של הרגולריזציה למשוואה נורמלית של רגרסיה ליניארית תיראה כך:
$\theta = (X^T\,X + \lambda\cdot L)^{-1} X^Ty $
$L = \begin{pmatrix} 0 & & & & \\ & 1 & & & \\ & & 1 & & \\ & & & \ddots & \\ & & & & 1 \end{pmatrix}$
מטריצה L היא בגודל n+1 x n+1 (כn הוא מספר המאפיינים), כשהאיבר הראשון באלכסון הוא 0, ואחריו כולם 1, כשכל שאר הערכים הם 0. זו פשוט מטריצה שיצרנו כדי להכפיל בה את למדא, ולקבל את הרגולריזציה שרצינו.
וגם כאן, ניתן לחשב ולראות שבעקבות המטריצה שהוספנו כל ערכי $\theta$ יקבלו ערך מעט קטן יותר ממה שהם היו אמורים להיות בסוף החישוב. בנוגע לבעיית אי ההפיכות שהזכרנו בנושא של משוואה נורמלית (מוזמנים להיזכר כאן), ניתן להוכיח שבמשוואה הנ"ל, עבור $m \le n$, אם למדא גדול מ0, המטריצה תהיה הפיכה ולא תהיה בעיה. למקרים אחרים $(m>n)$ היא תהיה עדיין בעייתית.
לגבי רגרסיה לוגיסטית, פונקציית העלות שלו תראה כך:
$ J(\theta) =\frac{1}{m} \sum_{i=1}^m [-y^{(i)} \log(h_\theta(x^{(i)})) –(1-y^{(i)})\log(1 – h_\theta(x^{(i)}))] $
$ \qquad + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2 $
כשגם כאן הסיגמא השנייה היא הרגולריזציה שהוספנו. שימו לב שj בסיגמא של הרגולריזציה מתחיל מ1 ולא מאפס. המשמעות היא שאנחנו מדלגים על $\theta_0$, כמו בנוסחה למעלה לרגולריזציה לרגרסיה ליניארית.
וגם כאן, אלגוריתם מורד הגרדיאנט ייראה דומה למורד הגרדיאנט של הרגרסיה הליניארית.
יאללה חלאס עם שבוע 3. למעבר לשבוע הרביעי, לחצו כאן!
שאלה\הערה\הראתי לסבתא? כתבו לנו בתגובות למטה

