שבוע 4
אם פספסתם משהו או סתם לא זוכרים, לחצו כאן כדי לעבור לשבוע 3.
הערה – אם אתם גולשים מהנייד, חלק מהנוסחאות עלולות "להימרח" לצדדים. סובבו את המכשיר לרוחב אם זה קורה.
גבירותיי ורבותיי, נוירונים:
רשתות נוירונים Neural Networks
רשתות נוירונים היא שיטת למידת מכונה ישנה שקמה מהמתים והתגלתה כמתאימה לבעיות מורכבות של סיווג לא ליניארי. היא הייתה בשימוש רב בשנות ה80 ותחילת ה90 ודעכה מאז לאט לאט עד לגילויה מחדש. הסיבה המקורית לפיתוח אלגוריתמי רשתות הנוירונים השונים הייתה לחכות את פעולת המוח, אך רק לאחרונה בגלל עוצמת החישוב של המחשבים של ימינו היא אפשרית בממדים גדולים.
נניח שיש לנו בעיית סיווג לא ליניארית שבה אנו רוצים לדעת האם הבית שלנו יימכר בחצי שנה הקרובה. בהרבה בעיות למידת מכונה, n שלנו יהיה גדול, ולכן בדוגמה שלנו כדי לקבל צורות שיתאימו מאוד טוב לסיווג יידרשו להמון כפילויות של מאפיינים (כל מאפיין בריבוע, וכפול כל מאפיין אחר וכולי). פתרון כזה יעלה המון זמן ומשאבים לחישוב.
ראייה ממוחשבת היא התחום בו גורמים למחשב להצליח "לראות" ומכך לזהות ולהסיק דברים מאמצעים חזותיים (תמונות, סרטונים, מציאות). להרבה אנשים לא ברור מה כה קשה למחשב לזהות מכונית לדוגמא כשלנו זה קל, אך צריך לזכור שהמחשב רואה זאת למעשה כל פיקסל כערך וצריך להבין מתוך אלפי פיקסלים מה החיבור שלהם נותן. כשכל פיקסל הוא מאפיין אנו מגיעים מהר לכמות ענקית של מאפיינים וגם כאן רגרסיה תהיה יקרה לחישוב.
בניסוי שנערך בעבר בחיות, ניתקו את העצב המקשר בין האוזן לחלק במוח האחראי על שמיעה. חיברו את העצב לעיניים, והתגלה שהחיות למדו לראות – למרות שזה לא היה תפקידו המקורי. מכך ומניסויים דומים התקבלו חיזוקים להיפותזת ה"אלגוריתם למידה יחידי", שטוענת שיש אלגוריתם אחד דרכו המוח לומד דברים חדשים ללא קשר לסוג הדבר שנלמד.
עוד כמה דוגמות הן Brainport – טכניקה לראות דרך הלשון, הדהוד אנושי במרחב (human echolocation) – הפקת קולות עצמית שעוזרת להתמצא במרחב בדומה לסונאר, חגורה ששולחת פולסים חשמליים ונותנת הרגשה של כיוון, וניסוי של השתלת עין שלישית בצפרדע שלמדה לראות בה.
תיאור המודל
קצת יותר מושגים והסברים ממה שהיה עד עכשיו, אבל לא מסובך. נתחיל מהבסיס:
תא עצב (נוירון) במוח בנוי בצורה הבאה: דנדריט(ים) (Dendrite), שהם מין חוטים שמעבירים מידע אל התא. אקסון ((Axon, שהם החוטים שמעבירים מידע החוצה מהתא, וגוף התא, שמכיל את הגרעין של התא ואחראי לקליטת מידע מהדנדריטים ושליחתו דרך האקסון כשעובר רף חשמלי מסוים (תאי עצב מעבירים אותות חשמליים מאחד לשני, למי שפחות בקיא).
אם נפשיט את הסיפור, אפשר להסתכל על כל תא עצב כיחידת חישוב שמקבלת כמה קלטים (הדנדריטים), מבצעת חישוב כלשהו (בגוף התא) ומוציאה פלט (שולחת אות דרך האקסון). במודל שלנו, הדנדריטים יהיו מאפייני הקלט x, והפלט כהיפתוזה h. הפונקציה עצמה תהיה דומה לפונקציה הלוגיסטית (הסיגמואיד) שראינו, $\frac{1}{1+e^{-\theta T x}}$, ותיקרא לרוב פונקציית ההפעלה (activation function).
בשכבה הראשונה, שכבת הקלט (input layer), יהיו מספר חיבורים כמספר המאפיינים, שישלחו עבור כל תצפית את הערכים שלה לנוירונים בשכבה השנייה, שימשיכו להיות מקושרים לשכבות נוספות עד לשכבה האחרונה שנקראת שכבת הפלט (output layer). כל השכבות שבאמצע נקראות שכבות נסתרות (hidden layers). רשת נוירונים תורכב ממספר שכבות של יחידות כאלו שמחוברות ביניהם.
החישוב בכל נוירון מתבצע כך: בדומה למה שלמדנו על פרמטרים, לכל חוט קלט יהיה "משקל" (weight) מסוים, שנקרא כך כיוון שהוא אומר למעשה כמה משקל אני נותן לקלט הזה. מכפילים כל קלט במשקל החוט שלו ומחברים. את התוצאה נכניס לh שלנו לפונקציית ההפעלה a, ובחיקוי לנוירון אמיתי תחזיר 1 במידה והערך יעבוד רף מסוים ו 0 אחרת. לכל שורה נוסיף חיבור $x_0$ שגם כאן ערכו תמיד יהיה שווה ל1. לרוב הוא נקרא bias unit (וואלה, איזה שם מקורי).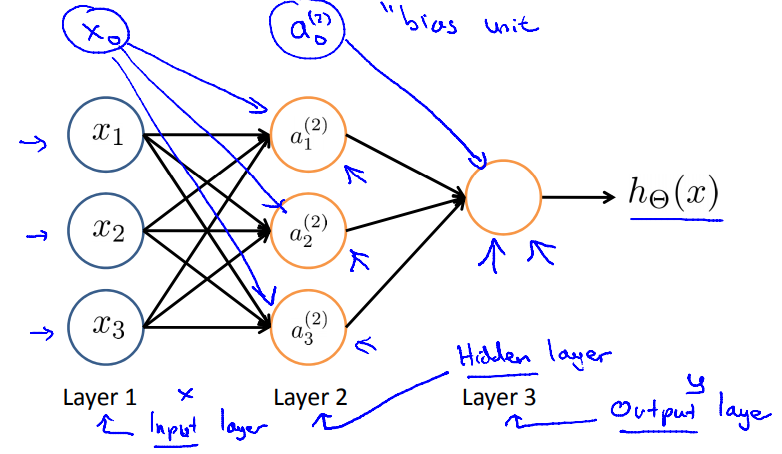
נסמן:
$a_i^{(j)}$ – "ההפעלה" של יחידת החישוב i, בשכבה j. הכוונה היא לערך עצמו שהתקבל מהפונקציה. a כמו activation.
$\Theta^{(j)}$ – מטריצת המשקלים של הפונקציה שעוברת משכבה j לשכבה j+1. הגודל של כל מטריצה כזו תהיה מספר השכבת בשכבה הבאה, כפול מספר השכבות בשכבה הבאה בתוספת 1 (bias unit). כדוגמה, אם בשכבה הנוכחית יש 3 יחידות ובהבאה יש 6, נקבל מטריצה בגודל 6×4. תעברו על הפסקה הזו טוב ותראו שאתם מבינים את המבנה של ה$\Theta$ ואת הדוגמה.
אם הייתה לנו שכבה נסתרת אחת (כמו בתמונה), התהליך היה נראה ככה:
$$[x_0, x_1, x_2, x_3] \to [a_1^{(2)}, a_2^{(2)}, a_3^{(2)}]\to h_\theta(x)$$
סיכום התהליך ואינטואיציה
לסכם – שכבה ראשונה היא הקלטים לפי המאפיינים, אליה מכניסים את התצפיות שלנו. אחריה נעשית ההפעלה של יחידות החישוב בשכבה הנסתרת, ומשם לשכבת הפלט שהתוצאה היא ההיפותזה שלנו. למעשה, אנחנו "מפיצים" קדימה את התצפית שלנו דרך הרשת – מה שנתן לתהליך הזה את השם אלגוריתם ההפצה קדימה (Feedforward propagation).
ניתן גם פה לשים לב, שניתן לערוך וקטוריזציה ובמקום לחשב אחד אחד ($x_i$ כפול המשקל שלו, וכן הלאה), אפשר לקצר תהליכים ופשוט להכפיל את הת'טה בכל הa כדי לקבל את התוצאה של השכבה הבאה. אם לכתוב את זה פורמלית, זה ייראה ככה:
$$z^{(j)} = \Theta^{(j-1)}a^{(j-1)}$$
הכפל בין הת'טות של שכבה j-1 בהפעלות שהתקבלו פשוט ייתנו את $z^{(j)}$, שנסמן כתוצאה של השכבה הבאה. כעת, $a^{(j)}= g(z^{(j)})$ וכן הלאה עד לשכבת הפלט (הכוונה בg היא לפונקציית הסיגמואיד כמובן).
אם נעצור רגע ונסתכל על השכבה האחרונה מחד, ועל שאר השכבות מאידך כשני חלקים נפרדים – נוכל להבחין שבשכבה הסופית אנו למעשה מקבלים מספר מאפיינים, עורכים עליהם פונקציה זהה לרגרסיה לוגיסטית ומקבלים תוצאה.
אך בניגוד לרגרסיה לוגיסטית, בעזרת החישובים של שאר השכבות שלקחו בהתחלה את המאפיינים המקוריים והפעילו עליהם חישובים שונים, נקבל מאפיינים יותר מורכבים, מה שבעצם עוזר למודל שלנו לחזות את הסיווג יותר טוב מרגרסיה פשוטה.
נקודה חשובה לגבי הפלט היא שצריך שכל אפשרות סיווג תהיה ייחודית – כך שאם נניח וישנם 4 נוירוני פלט ל4 קבוצות שונות, הפלט שיחזה את סיווג לקבוצה הראשונה יהיה 1 בנוירון הראשון ו0 בשאר:
$y=[1,0,0,0]$, וכן הלאה לפי הסדר – $[0,1,0,0]$ וכולי. החשיבות היא כיוון שאנחנו רוצים למצוא הבדל מהותי בין הקבוצות – לדעת שכל תצפית תהיה שייכת לקבוצה אחת בלבד. במצב של פלט בינארי (רק 2 קבוצות) אפשר להסתפק רק בנוירון פלט אחד, כי כל מספר שולל בהכרח את האחר.
דוגמה
כדי לחזק עוד יותר את האינטואיציה מאחורי כל הבלאגן הזה, נתחיל מדוגמה לחישוב פונקציית "או". נניח ש$x_0,x_1$ מקבלים רק 0 או1 (כמו במעגל לוגי, לדוגמה), ונצייר:

הפונקציה שאנו מחשבים נראית כך:
$$g(-10 * bias + 20 * x_1 + 20 * x_2) $$
נוכל לשים לב לפי הטבלה, שלפי הערכים שמוכנסים, הפלט הסופי של h מתאים בדיוק לOR. ניקח כדוגמה את השורה השנייה – רק $x_2$ מופעל ולכן נקבל $g(10)$ ששווה ל1. בהתאם אפשר לבדוק בקלות את השאר. ניתן בצורה דומה לבנות גם פונקציית "וגם" (נסו לחשוב עם איזה ערכים של משקולות כדי להתאים את זה לAND). מחיבורים מעבר לשכבה אחת ניתן ליצור פונקציות מרוכבות יותר.
אחרי שהבנתם את הדרך לבנות פונקציית "וגם" (תשובה במוסתר: לשים משקל של -30 ביחידת bias. כמובן שזו לא התשובה היחידה), נסו לבנות פונקציות בדרגה אחת גבוהה יותר, כמו XNOR או XOR.

