קורס למידת מכונה – שבוע 5: רשתות נוירונים, פעפוע לאחור ומימוש

רוצים להיות מעודכנים בכל מה שעולה ולא לפספס שום דבר? הרשמו למינוי למייל: (שימו לב - אם נרשמתם ל"הכל", לא צריך לסמן גם את השאר - אתם סתם תקבלו מיילים כפולים)

שם*

אימייל*

Lists*

הכל

בינה מלאכותית וML

שבוע 5

אם פספסתם משהו או סתם לא זוכרים, לחצו כאן כדי לעבור לשבוע 4.

הערה – אם אתם גולשים מהנייד, חלק מהנוסחאות עלולות "להימרח" לצדדים. סובבו את המכשיר לרוחב אם זה קורה.

לאחר שעסקנו ברשת הנוירונים עצמה, נעסוק כעת באיך להתאים את הפרמטרים לסט אימון שיש לנו. נסמן $L$ כמספר השכבות ברשת ו$S_1$ כמספר היחידות בשכבה $l$, וכמו בשבועות קודמים נחלק למקרה הבינארי (2 פלטים אפשרים) עם יחידת פלט אחת, ולמקרה הכללי עם $k$ אפשרויות ו$k$ יחידות פלט (כיוון שאנו רוצים יחידה ייחודית לכל אפשרות).

פונקציית העלות Cost Function

פונקציית העלות תהיה הכללה של הפונקציה מרגרסיה לוגיסטית:

$\begin{align} J(\Theta) & = -\frac{1}{m} [ \sum_{i=1}^m \sum_{k=1}^K y_k^{(i)} \log{(h_\Theta(x^{(i)}))}_k + (1 – y_k^{(i)})\log{1 – (h_\Theta(x^{(i)}))}_k \\ & + \frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{i=j}^{s_l+1} (\Theta_{ji}^{(l)})^2 \end{align}$

כאשר הסוגריים הראשונים הם בדיוק כמו ברגרסיה הלוגיסטית, רק שברשתות נוירונים כיוון שכל יחידת פלט היא ייחודית עלינו לחשב את הפונקציה לכל אחת מ$K$ האפשרויות (האינטואיציה היא לשים לב שה$y$ שמתקבל מהרשת הוא וקטור ולא ערך יחיד כמו ברגרסיה, כך שיש לעבור כמספר האיברים של $y$ שהן למעשה מס' האפשרויות). הביטוי השני הוא הרגולריזציה של הפרמטרים שאצלנו הם מטריצות המשקלים של כל היחידות ברשת.

כמו במורד הגרדיאנט וכל אלגוריתם לחישוב העלות המינימלית, עלינו לחשב 2 דברים כדי להתאים את הפרמטרים שלנו: את פונקציית העלות עצמה, ואת הנגזרות החלקיות שלה לפי כל $i,j$. עם קצת פורמליקה –

$\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)$

פעפוע לאחור Backpropagation Algorithm

הרעיון פשוט אבל יש הרבה נוסחאות, אז נתחיל מדוגמה שבה יש לנו רק תצפית אחת, ומתוכה נסביר את הרעיון. אחר כך נרחיב למקרה הרגיל עם מספר רב של דוגמות.

אז ככה – כדי לחשב את הפרמטרים של כל יחידה ברשת, נשתמש ברעיון של פעפוע לאחור – נחשב תחילה את הערך שיוצא לנו כעת בחישוב רגיל. לאחר מכן, נתחיל מהשכבה האחרונה (פלט) ונחשב לכל יחידה את הפרש הטעות בין מה שציפינו שייצא, לבין מה שיצא מאותה יחידה. נניח שציפינו לקבל על דוגמה מסוימת שהיא שייכת לקבוצה "1", אבל האלגוריתם אמר שהיא שייכת ל"0". ניקח את הפרש הטעות (1) ונחשב מחדש מה אמור להיות משקלי הקשתות בשכבה שלפני הפלט, שהובילו ליחידת הפלט. כעת נמשיך לחשב אחורה עד שנגיע לשכבת הקלט.

האינטואיציה לדבר היא בכך שאם נשים לב, נראה שלכל אחת מיחידות האימון יש איזו שהיא "טעות" שביחד גרמה ליחידות הפלט להוציא תוצאה שלא מתאימה לפלט המקורי שלנו מסט האימון. באלגוריתם הנ"ל אנחנו חוזרים אחורה ומתקנים כל יחידה לפי ההפרש בין התוצאה שהתקבלה בה, לבין התוצאה שאמורה הייתה להיות לפי סט האימון.

הדרך הכי טובה להסביר את האלגוריתם היא לחשוב בדיוק על ההפך מתהליך הלמידה של הרשת – עד עכשיו הכנסנו תצפיות, חישבנו את ערכי ההפעלה של כל יחידה כפול הקשתות שלה והעברנו אותם כקלט הלאה והלאה, עד שהגענו לשכבת הפלט והוצאנו תשובה. כעת, אנחנו שוב מחשבים את הערכים אחורה – אנחנו מקבלים פלט, לוקחים את ההפרש (שהוא הטעות שלנו), ומכפילים במשקולות שגרמו לאותה טעות להופיע.

נעבור לאלגוריתם למקרה הכללי – בדיוק אותו דבר, רק שכעת נזכור את ה"טעות" לכל תצפית ונחבר אותן. לא להיבהל: אתם הולכים לראות הרבה מתמטיקה, אבל נסביר הכל.

נסמן $\triangle_{ij}^{(l)}$– להיות מטריצת החישוב שלנו. בהתחלה כל הערכים יהיו 0.

ועכשיו, עבור כל דוגמה $t$ מסט האימון:

1. $a^{(1)} = x^{(i)}$
2. נפעיל אלגוריתם הרצה קדימה (וממנו נחשב את כל ה$a$ לכל שכבה)
3. עכשיו, מהסוף להתחלה – נחשב לשכבת הפלט את $\delta^{(L)} = a^{(L)} – y^{(t)}$. ועבור כל שכבה $l$ אחרת (לא כולל שכבת הקלט, כי אין שם טעות – זה הקלט עצמו) נחשב:

$\delta^{(l)} = (\Theta^{(l)})^T\delta^{(l+1)}.*g'(z^{(l)})$

עם קצת אינפי אפשר להפוך את הנגזרת של g ולקבל:

$\delta^{(l)} = (\Theta^{(l)})^T\delta^{(l+1)}.*a^{(l)}.*(1-a^{(l)})$

(המשמעות של הכפל עם הנקודה היא להכפיל איבר באיבר – ולא לעשות הכפלת מטריצות)

4. $\triangle_{i,j}^{(l)} := \triangle_{i,j}^{(l)}+a_j^{(l)}\delta_i^{(l+1)}$, או עם וקטוריזציה: $\triangle_{i,j}^{(l)} := \triangle_{i,j}^{(l)} + \delta_i^{(l+1)} (a_j^{(l)})^T$

נסיים את הלולאה, ונחשב את המטריצה הבאה:

$ \begin{align} & D_{ij}^{(l)}:= \frac{1}{m}\triangle_{i,j}^{(l)} + \lambda \Theta{ij}^{(l)} \quad \text{if j != 0} \\ & D_{ij}^{(l)}:= \frac{1}{m}\triangle_{i,j}^{(l)} \quad \text{if j=0} \end{align} $

תמונה להמחשה של חישובי הדלתא ברשת לדוגמה:

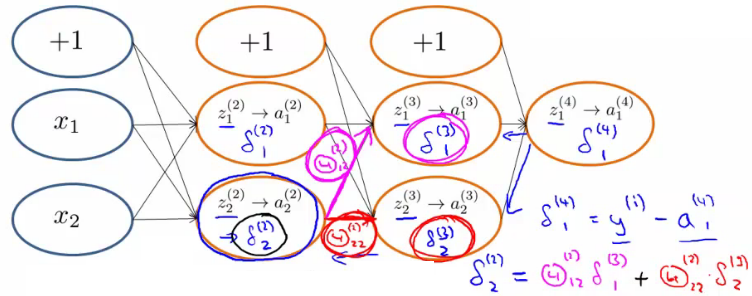
הסבר והערות:

אם נסתכל טוב על הנוסחה בשלב 3, היא למעשה אותו חישוב של הפרש הטעות: אנחנו לוקחים את הטעות מהשכבה הבאה $(l+1)$, ומכפילים אותה בערכי המשקולות שלה. את כל זה אנחנו מכפילים בנגזרת של הפונקציה $g$ שדרכה קיבלנו את הערכים שלנו כדי לקבל את הטעות ביחס לערכים שיצאו מהשכבה הנוכחית. המשך הפיתוח של הנוסחה יכול להסגיר קצת מהאינטואיציה הזו, למרות שבתכלס הוא רק משמש לחישוב נוח יותר של הנוסחא.

הנוסחה בשלב 4 היא בסך הכל הוספה של ערכי הטעות שהתקבלו מכל דוגמה.

בסיום הלולאה, קיבלנו בכל תא בΔ את ערך הנגזרת החלקית המצטברת לכל סט האימון. כדי להסתכל על זה ביחס לדוגמה אחת, נחלק ב$m$ ונוסיף רגולריזציה לביטוי במידת הצורך (כש$j$ לא שווה ל0). ובסך הכל, נקבל המטריצה $D$ היא בדיוק מה שרצינו לחשב. או במילים אחרות:

$\frac{\partial}{\partial \Theta{ij}^{(l)}} J(\Theta) = D_{ij}^{(l)}$

הללויה.

בדיקת הגרדיאנט Gradient Cheking

אלגוריתם הפעפוע לאחור הוא אמנם אולי פשוט כרעיון, אבל הוא יותר מסובך כמימוש והרבה פעמים יוצא שבגלל באגים קטנים תוצאות האלגוריתם שמממשים אינן הכי טובות שאפשר, גם אם רואים שפונקציית העלות ממשיכה לקטון. שיטת בדיקת הגרדיאנט מנסה לפתור את כל הבעיות שעלולות לצוץ במהלך בניית האלגוריתם כדי להיות בטוחים שהוא ממומש בצורה הכי טובה.

הקטע של בדיקת הגרדיאנט הוא בדיוק כמו השם שלו – אנחנו נבדוק לפני ההפעלה של אלגוריתם הפעפוע לאחור מה אמורים להיות ערכי השיפוע שאנחנו מנסים לקבל, ואם נקבל פחות או יותר את אותם הערכים נבין שמימשנו את האלגוריתם בשיטה הנכונה. הפרוצדורה מאוד פשוטה:

$\frac{\partial}{\partial\Theta}J(\Theta) \approx \frac{J(\Theta+\epsilon) – J(\Theta-\epsilon)}{2\epsilon}$

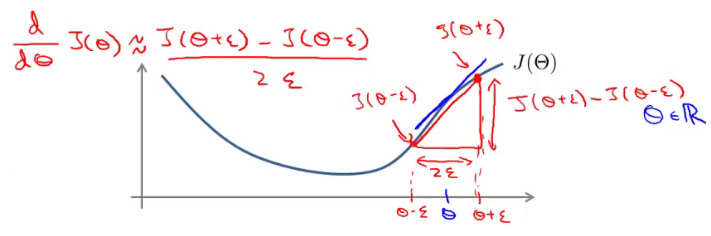
אנחנו לוקחים את ה$J(\Theta)$ שהייתה אמורה לצאת לנו, ובודקים "מסביב": בודקים את ההפרש כשמוסיפים אפסילון מימין ל$J$, מול המצב כשמורידים אפסילון משמאל. את התוצאה מחלקים בטווח (שהוא 2 אפסילון), וכך מקבלים קירוב של אותו השיפוע שאמור להיות בנקודה המקורית שלנו, $J(\Theta)$. המחבר (אנדרו) ממליץ להשתמש בערכי אפסילון נמוכים כמו 10^-4 אבל לא נמוכים מידי, כיוון שזה יכול לגרום לבעיות חישוב מתמטיות. את הטריק הזה עושים לכל אחת ממטריצות המשקלים שלנו, ולכן הנוסחה נראית ככה:

$$\frac{\partial}{\partial\Theta_j}J(\Theta) \approx \frac{J(\Theta_1,…,\Theta_j+\epsilon,…,\Theta_n) – J(\Theta_1,…,\Theta_j-\epsilon,…,\Theta_n)}{2\epsilon}$$

עבור $\Theta_j$ מסוים.

חשוב לציין שאת הבדיקה הזאת מספיק לעשות פעם אחת – ברגע שאנחנו רואים שהתוצאה שקיבלנו הן מאוד קרובות למה שנתן אלגוריתם הפעפוע, אפשר להיות דיי רגועים שהמימוש שלנו הצליח ואין צורך לחשב את הבדיקה שוב ושוב. מה גם שהבדיקה הזו היא מאוד איטית מבחינת זמן ריצה, לעומת אלגוריתם הפעפוע לאחור שפועל באופן מדויק ומהיר יותר.

אתחול רנדומלי Initial Randomization

הנקודה האחרונה בבניית אלגוריתם הפעפוע לאחור היא הדרך שבה אנחנו מאתחלים את $\Theta$, דהיינו את המשקולות של הרשת. ברגרסיה לוגיסטית אמנם יכולנו לאתחל איך שבא לנו (וספציפית אתחלנו את כל המטריצה כאפסים, בשבוע 3), אבל ברשת נוירונים הדבר הזה לא יעבוד.

אתחול של כל המשקולות לאותם ערכים, יגרום לכך שהפונקציות שיתקבלו ברשת לכל יחידה יהיו שוות אחת לשנייה, ובמקום ליהנות מהיתרון של הרשת היא פשוט תהיה אותה פונקציה כל הזמן. הפתרון הוא לקבוע ערך אפסילון כלשהו (לא קשור לאפסילון של בדיקת הגרדיאנט, זה אחד חדש), ולתת לכל המשקולות ערך רנדומלי בין $[-e,e]$. בצורה הזו הערכים המתקבלים ברשת יהיו שונים אחד בשני ויוכלו לייצג כל אחד מהמאפיינים שלנו כמו שצריך.

בניית האלגוריתם

סיימנו ללמוד על הדרך שבה רשת הנוירונים לומדת. בואו נארגן את כל מה שקרה פה:

בהתחלה, עלינו לבחור ארכיטקטורה לרשת. יש שני דברים קבועים בנושא – מספר היחידות בשכבת הקלט הוא מספר המאפיינים, ומספר יחידות הפלט הוא לפי ערכי y השונים (חוץ ממצב בו יש רק 2 קבוצות, אז מספיק רק יחידה אחת שתגיד אם הוא מהקבוצה הראשונה או לא). כל זה בדיוק כמו שלמדנו בשיעורים הקודמים. לגבי השכבות הנסתרות – לרוב אנדרו אומר שאפשר להסתדר עם שכבה אחת נסתרת. אם עושים יותר משכבה אחת, בדרך כלל נותנים לכל השכבות הנסתרות את אותו מספר הנוירונים. באופן כללי הוספת שכבות זה דבר טוב, אבל חשוב לזכור שכל הוספה של שכבה (ויחידות) יכולה להיות מאוד יקרה לחישוב (מבחינת זמן).

אחרי שבחרנו את הארכיטקטורה שלנו, נחבר את כל השלבים:

1. אתחול רנדומלי של המשקולות. בדרך כלל לערכים שקרובים ל0.
2. נממש את ההפצה קדימה (Feedforward propagation) כדי לקבל את ההיפותזות שלנו לכל תצפית $x^{(i)}$
3. נממש קוד לחישוב פונקציית העלות $J(\Theta)$ (Cost Function).
4. נממש את אלגוריתם הפעפוע לאחור (Back propagation) לפחות בפעם הראשונה, נבנה אותו עם לולאה שעוברת תצפית תצפית ומעבירה אותה אחורה וקדימה ברשת הנוירונים שלנו. במידע שנקבל, נשתמש כדי לחשב את הנגזרות החלקיות של פונקציית העלות, ולדעת כמה ואיפה טעינו.
5. נשתמש בבדיקת הגרדיאנט ונחשב את פונקציית העלות שוב, ונשווה בין מה שקיבלנו לתוצאה שקיבלנו בסעיף 4, כדי לראות שאנחנו בכיוון הנכון. זכרו לבטל\לזרוק את הבדיקה אחרי פעם אחת כי כבר אין בה צורך והיא לוקחת מלאא זמן.
6. כעת נשתמש באחת משיטות האופטימיזציה, כמו מורד הגרדיאנט (Gradient Descent) שלמדנו לדוגמה, ביחד עם אלגוריתם הפעפוע לאחור, כדי לנסות להקטין את $J(\Theta)$ כפונקציה של $\Theta$, ולהביא אותה למינימום – בעיית מינימיזציה.

נקודה טיפה מבאסת – הזכרנו בהתחלה ממש בקצרה שפונקציית העלות של רגרסיה ליניארית היא קונבקסית, שבתכלס מה שזה אומר, זה שמובטח לנו שאם הגענו למינימום – זה המינימום האופטימלי. הבאסה עם פונקציית העלות שלנו ברשת נוירונים היא שהיא לא קונבקסית, ולכן בתיאוריה אנחנו לא יכולים להיות בטוחים שכשנגיע לנקודת מינימום כלשהי, היא באמת תהיה נקודת מינימום גלובלית.

נקודת אור בכל הסיפור הזה, היא שבפועל אלגוריתם הפעפוע לאחור ופונקציית העלות שלנו כן מביאה לתוצאות טובות מאוד, גם אם אי אפשר להבטיח שהן הכי טובות שיכלו להיות. מסיבה זו לפעמים נוהגים לאתחל את המשקולות כמה פעמים ולראות לאיזה נקודות הרשת תיקח אותנו בכל פעם.

יאללה תחייכו סיימנו את השבוע! לשבוע 6, לחצו כאן.