שבוע 6 א'
אם פספסתם משהו או סתם לא זוכרים, לחצו כאן כדי לעבור לשבוע 5.
הערה – אם אתם גולשים מהנייד, חלק מהנוסחאות עלולות "להימרח" לצדדים. סובבו את המכשיר לרוחב אם זה קורה.
יש בקורס הזה כמה שבועות קצת יותר ארוכים מהרגיל, זה אחד מהם. החלטנו לחלק אותו לשני חלקים כדי להקל בקריאה שלו (תאמינו לי שאנחנו לא נהנים לכתוב כ"כ הרבה, כתוב כאן כל מה שצריך לדעת).
הקדמה
אחרי שלמדנו מספר יפה של אלגוריתמים וטכניקות למידת מכונה, השבוע נתמקד בהבנה, טיפים והצעות למימוש שלהם במצבים שונים, ובייחוד לגבי ההבנה של איזה דרכים לקחת כאשר קיימת כבר מערכת למידת מכונה ואנחנו רוצים לשפר אותה.
בואו נחזור לשבוע 1 ונניח שמימשתם רגרסיה ליניארית עם רגולריזציה כדי לחזות מחירי בתים. הכל עובד יופי עד שאתם מריצים את ההיפותזה שקיבלתם על סט חדש של בתים ומגלים שהחיזוי הוא על הפנים. מה הייתם עושים – משיגים עוד תצפיות? מורידים מאפיינים? מוסיפים מאפיינים? מוסיפים מאפיינים פולינומים ($x_1^2$ וכו')? משחקים עם הלמדא של הרגולריזציה?
כל הרעיונות האלו הם סבבה, באמת. אבל כדי לא למצוא את עצמכם מבזבזים חצי שנה על איסוף דאטה רק כי "תחושת בטן" אמרה לכם שצריך לתייק את כל הבתים בגוש דן ובסוף לגלות שזה לא עזר (חוץ מלדעת כמה עולה הבית של חמותי עלק אין לך כסף רותי), יש צורך אמיתי להבין כיצד לאבחן את המודל כדי לדעת איזה שביל לקחת. נתחיל בלהבין איך להעריך ביצועים של אלגוריתם, ונמשיך לדבר על טכניקות אבחון ובדיקות לאלגוריתמי למידת מכונה.
הערכת האלגוריתם Evaluating the Algorithm
המחשבה שמספיק שיהיה לנו אחוז טעות נמוך (J מינימלי) אינה בהכרח נכונה. מקרים של התאמת-יתר (overfitting) קורים דווקא כשההיפותזה חוזה בדיוק רב את סט התצפיות אבל נכשלת בדוגמות חדשות. כשיש לנו מאפיין אחד או שניים, אפשר בקלות להדפיס גרף שייראה את ההיפתוזה שקיבלנו ודרכה להבין אם דבר כזה קרה, אבל עבור מספר מאפיינים גבוה יותר השיטה הזו נהיית קשה עד בלתי אפשרית. נצטרך דרך אחרת, והיא תהיה חילוק של התצפיות שלנו לשני חלקים.
חלק אחד, שיקרא סט האימון (training set) כמו שהיה לנו עד עכשיו – אבל הפעם הוא יהיה רק חלק מהתצפיות שיש לנו, וסט הבדיקה (test set) שיכיל את התצפיות הנותרות. חילוק לדוגמה יכול לקחת 70% מהתצפיות לסט האימון ו30% לבדיקה, אבל אפשר לשחק עם זה. חשוב לשים לב שאם מאגר התצפיות מסודר או מדורג, צריך לקחת תצפיות רנדומליות או לערבב את כל התצפיות כדי לשמור על גיוון בשני הסטים.
כעת, הלמידה שלנו תעבוד בצורה הבאה:
- נחשב כרגיל את $\Theta$ ולצמצם את $J_{train}(\Theta)$.
- נחשב את $J_{test}(\Theta)$. מה שקורה כאן בעצם הוא שאנחנו מתאמנים רק על סט האימון, ומשתמשים בת'טות שקיבלנו את לחשב את הטעות על סט תצפיות הבדיקה.
הנוסחה לחישוב של $J_{test}$ ו$J_{train}$ היא כמובן אותה נוסחה בדיוק. לדוגמה ברגרסיה ליניארית היא תיראה כך:
$$ J_{test}(\Theta) = \frac{1}{2m_{test}} \sum_{i=1}^{m_{test}} (h_\Theta(x_{test}^{(i)}) – y_{test}^{(i)})^2$$
לבעיות סיווג, אפשר להשתמש בנוסחת הJ לרגרסיה לוגיסטית שלמדנו, או פשוט לספור כמה תצפיות מסט הבדיקה ההיפתוזה שלנו חזתה נכון וכמה לא. עבור רגרסיה לוגיסטית עם שתי קבוצות בלבד, זה ייראה ככה:
$$ Error = \frac{1}{m_{test}} \sum_{i=1}^{m_{test}}err(h_\Theta(x_{test}^{(i)}),y_{test}^{(i)})^2$$
כאשר הפונקציית $err$ פשוט מוציאה 1 במקרה שלא חזינו נכון (אם $h_\Theta(x)\ge 0.5$ כש$y=0$ או $h_\Theta(x)<0.5$ כש$y=1$).
בחילוק הזה, נוכל להעריך נכון את ההיפותזה שלנו על "העולם שבחוץ" – סט הבדיקה, ולגרום למודל לקלוע יותר למקרה הכללי.
עם זאת, כשעלינו לבחור בין מודלים או כשיש לנו מודל שתלוי בהיפר-פרמטרים (hyperparameters, הכוונה היא לפרמטרים שהם חיצוניים למודל, כמו הלמדא של הרגולריזציה, קצב למידה, מספר האיטרציות, דרגה פולינומית ועוד), ההמלצה היא לחלק את התצפיות שלנו דווקא ל3 חלקים – סט אימון, סט אימות (validation set) ובדיקה. חילוק של 60% אימון, 20% אימות ו20% בדיקה הוא דוגמה ליחס נפוץ, אך גם כאן ניתן לשחק עם המספרים.
הסיבה לפיצול הנוסף היא כזו – נניח שאנחנו רוצים לבחור איזה דרגה פולינומית להכניס לאלגוריתם הרגרסיה שלנו. בחרנו 10 דרגות (מ$x$ עד $x^10$), הרצנו אותם והגענו ל$J_{train}$ מינימלי. אם ננסה לקבוע איזה מהם הכי טוב על ידי חישוב של $J_{test}$, אנחנו עובדים על עצמנו – הרגע בחרנו את דרגת הפולינום של המודל בהתאם ל$J_{test}$ המינימלי שמצאנו! החישוב שביצענו כדי לקבוע את הדרגה הכי טובה התבצע על סט הבדיקה, ולכן המודל שוב עלול להיכשל ולייצר היפותזה "אופטימית" מידי שאינה נכונה למקרה הכללי. כדי להתגבר על הבעיה, נכניס את סט האימות שישמש בתוך "מתווך" – נריץ עליו את הבדיקות שעשינו, נקבע את המודל וההיפר פרמטרים שהכי טובים לנו, וכך סט הבדיקה יישאר נקי ולא משוחד לקביעת תוצאות האלגוריתם שלנו כמו מקודם.
אנדרו טוען שאפשר לפעמים להתחמק מהבעיה הזאת כאשר סט הבדיקה שלנו מספיק גדול, אבל אין ספק לדעתו שיש יותר מידי אנשים שעושים את הטעות הזו ומסתמכים על סט הבדיקה לדברים שסט האימות מיועד עבורם. השיטה הטובה ביותר במקרים כאלה היא אכן לחלק את התצפיות לשלושה סטים נפרדים.
אבחון האלגוריתם: הטיה מול שונות Algorithm Diagnostics: Bias vs. Variance
כמעט בכל הפעמים בהם ביצועי האלגוריתם שלכם לא היו ברמה אליה ציפיתם, הסיבה תהיה התאמת-חסר או התאמת-יתר, או במילים אחרות – במקרה שההיפותזה שלנו אינה מדויקת מספיק וסובלת מהתאמת חסר, תהיה לה הטיה גבוהה (high bias). במקרה שההיפותזה שלנו מדויקת מידי וכבר אינה טובה למקרה הכללי, תהיה לנו שונות גבוהה (high variance). אחת ההבחנות החשובות כשאנחנו מנתחים את ביצועי האלגוריתם היא להבין מאיזה סוג בעיה הוא סובל (אולי גם משניהם), ועד כמה.
למי שלא בא עם רקע בסטטיסטיקה, הנה הסבר על המילים בלי צורך בתואר: הצמד "הטיה" ו"שונות" נקראות כך, פשוט כי הן מתארות את מה שקורה בפועל במקרים האלו. חשבו על כל התצפיות כעל שורה מסודרת של ערכים ממוינים: בהתאמת-חסר, ההיפותזה כמעט אינה מתאימה לאף אחת מהתצפיות, ולכן ההטיה שלה (בנוגע לתצפיות) היא גבוהה – זרוק תצפית, תקבל y שגוי. מאידך, בהתאמת-יתר, כשהיא מתאימה מאוד לכל תצפית, הכל יהיה בסדר חוץ מהתצפיות ה"מוזרות" וה"רחוקות" שיקבלו ערכים מזעזעים, ולכן השונות שלה גבוהה (כמה היא "שונה" מהמרכז). הsweet-spot של כל אלגוריתם למידה הוא האיזון הרצוי ביניהם לפי המקרה שעליו עובדים.
עכשיו נחזור לדוגמה של הדרגה הפולינומית ממקודם כדי לקבל קצת אינטואיציה לגבי מתי כל אחת מהן קורית: נחשוב מה קורה ל$J_{train}$ ככל שמעלים את הדרגה – בדרגה פולינומית נמוכה, ההיפותזה שלנו תהיה פחות מדויקת ביחס לתצפיות, לכן נקבל ערך גבוה ל$J_{train}$. ככל שנעלה את הפולינום נתאים את ההיפותזה בצורה יותר מדויקת, ולכן הערך של $J_{train}$ יירד. קיבלנו מין "מגלשה".
לעומת זאת, אם נסתכל על $J_{val}$ (או $J_{test}$ במקרה שלא חילקנו ל3), נראה לרוב דבר קצת שונה – גם כאן, בדרגה נמוכה של הפולינום, נקבל $J_{val}$ גבוה – כי ההיפותזה לא מתאימה עדיין לא לסט האימון ולא לסטים האחרים. מצד שני, כשהדרגה של הפולינום היא גבוהה, היא מתאימה באופן כמעט מושלם לסט האימון, ולכן שוב נקבל עבור סט האימות\הבדיקה ערך J גבוה. בסך הכל, קיבלנו במקרה הזה מין פרבולה מחייכת.
כעת, השוואה פשוטה בין הערכים יכולה להסביר לנו איפה אנחנו עומדים – אם גם $J_{train}$ וגם $J_{val}$ גבוהים (ודיי שווים בערכם), כנראה שההיפותזה לא מתאימה בכלל לשום דבר ואנחנו מדברים על בעיית הטיה גבוהה. אם לעומת זאת $J_{train}$ נמוך או מינימלי אבל $J_{val}$ נשאר גבוה יחסית ממנו, אנחנו כנראה מדברים על בעיית שונות גבוהה.
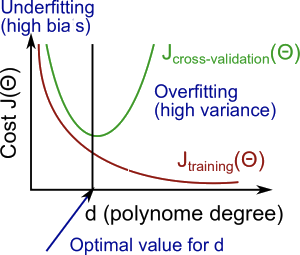
עוד דוגמה, הפעם רגולריזציה: נשים לב שמבחינת הגרף, נקבל תמונת "מראה" בגלל ה$\lambda$ – כשהלמדא נמוכה, היא כמעט לא משפיעה, לכן להיפותזה תהיה התאמת-יתר ונקבל $J_{train}$נמוך. כשהלמדא גבוהה, היא כמעט מוחקת את ה$/theta$ שקיבלנו ולכן יהיה $J_{train}$ גבוה.
כדי למצוא במקרה כזה את הלמדא המתאימה, דרוש "ניסוי וטעייה" – פשוט לנסות מספר ערכים וטווחים על המודלים שלנו עד שנגיע למה שעובד הכי טוב בשבילנו. בשלבים זה נראה ככה:
- ניצור רשימה של ערכי $\lambda$ (נניח {0,0.1,0.2,0.4..0.16..5.12})
- ניצור קבוצת מודלים שונים שנרצה לבדוק (נגיד מודלים פולינומליים עם דרגות שונות וכולי)
- נרוץ על כל $\lambda$, ועבור כל אחת נאמן את כל המודלים כדי לקבל מהם את ה$\Theta$ שלנו.
- נשתמש בת'טות השונות שקיבלנו כדי לחשב את השגיאה שלנו על סט האימות ($J_{val}$) – שימו לב שהחישוב הוא בלי רגולריזציה כי אחרת נעבוד על עצמנו כמו שהסברנו למעלה.
- נבחר את הקומבינציה הכי טובה (של פרמטרי מודל $\Theta$ ולמדא) שהביאה לנו את ה$J_{val}$ הכי נמוך, ונחשב איתם את ה$J_{test}(\Theta)$.
עקומת למידה Learning Curve
אחת השיטות הטובות ביותר כדי להבין מה מצב האלגוריתם, היא להדפיס כגרף את "עקומת הלמידה", דהיינו את ערכי הJ של הסטים השונים, אימון (אימות) ובדיקה, כפונקציה של $m$, מספר התצפיות. נניח שבחרנו אלגוריתם למידה:
נבחין, שכשיש לנו מספר תצפיות קטן, יותר קל למצוא היפותזה שתעבור בדיוק בכל הנקודות, ולכן $J_{train}$ יהיה קטן (או אפסי). כשנוסיף עוד ועוד תצפיות לסט האימון – J ייגדל, ולבסוף פחות או יותר יתכנס לערך מסוים (כי ברגע שיש כבר המון המון תצפיות וכבר קיבלנו את ההיפותזה הכי טובה האפשרית לאלגוריתם, עוד תצפית אחת בודדת כבר לא תשנה משהו). קיבלנו גרף בצורה כמו של פונקציית לוג (יעני האות ר' הפוכה = r).
מצד שני, הJ של סט האימות או הבדיקה ייראה כמו מראה – במידה והתאמנו על קצת תצפיות, נקבל ערך גרוע מאוד ל$J_{val}$/$J_{test}$ (כי התאמנו על סט האימון, ומה כבר היפותזה על כמה נקודות בודדות באימון יכולה לומר על כל נקודות בודדות שונות?). אבל ככל שנגדיל את את מספר התצפיות שהתאמנו עליהן, יתחיל J להתכנס לערך נמוך יותר – כי במצב של הרבה תצפיות, ההיפותזה תדע יותר להתכוונן למקרה הכללי.
"אוקיי אחי. ואיך זה מתקשר לנו להטיה ולשונות?" נפרק לפי מקרים, ונחשוב מה כל אחד מהם אומר:
נתחיל בלדמיין מקרה של אלגוריתם שסובל מהטיה גבוהה (התאמת-חסר): במקרה כזה, נסבול מהיפותזה "כללית" מידי, שלא מצליחה להעביר קו מדויק מספיק לכל התצפיות. $J_{train}$ אמנם יהיה נמוך למס' תצפיות קטן כמו שאמרנו, אבל ככל שנוסיף תצפיות נקבל גרף שמתכנס לערך מאוד גבוה של J. כנ"ל לגבי $J_{test}$ – נתחיל מערך גבוה אבל נתכנס גם פחות או יותר לאותו ערך J של $J_{train}$. פשוט כי ההיפותזה שלנו מוטה מידי לכל תצפית. נסתכל על משהו כזה:
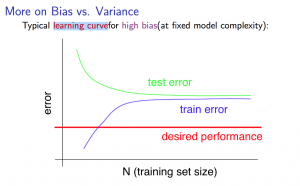
במקרה כזה, חשוב להבין שגם אם נוסיף טריליון תצפיות (אולי הגזמתי קצת), זה כנראה לא יפתור לבדו את ערך השגיאה הגבוה. האלגוריתם שלנו פשוט לא מתאים מספיק כדי לתת כאן היפותזה מדויקת יותר למקרה שאנחנו עוסקים בו.
נעבור למקרה של שונות גבוהה (התאמת-יתר): במקרה זה, נסבול מהיפותזה מדויקת מידי, ולכן $J_{train}$ יתחיל נמוך אבל יישאר נמוך וכנראה גם ייתכנס לערך נמוך – ההיפותזה של האלגוריתם פשוט מסוגלת להתאים (כמעט) את כל התצפיות של סט האימון. מצד שני, העובדה שאנחנו מתאמנים על סט האימון לא תעזור ל$J_{test}$/$J_{val}$ יותר מידי, והם גם יתחילו גבוה וירדו לאט לאט, אבל עדיין יהיו גבוהים יותר מ$J_{train}$ – למעשה, שלא כמו במקרה של הטיה, נוצר לנו כאן מרווח (gap) בין הערכים:
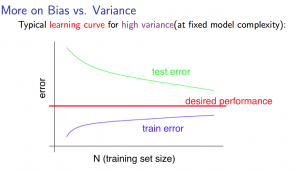
במקרה כזה, אפשר כבר לזהות מגמה – ככל שאנחנו מגדילים את מספר התצפיות, הערכים שואפים זה לזה. ולכן, במקרה של שונות גבוהה, ליקוט והוספה של עוד תצפיות עשוי לעזור.
לסיכום: במצב של הטיה גבוהה (high bias), נקבל לרוב ש$J_{train}$ פחות או יותר שווה ל$J_{test}$/$J_{val}$, ושניהם גבוהים. במצב של שונות גבוהה (high variance), נקבל לרוב ש$J_{train}$ נמוך יחסית, וקיים בינו לבין $J_{test}$/$J_{val}$ הפרש יחסי, או "מרווח".
ובחזרה להערכת האלגוריתם
אמרנו שיש כל מיני אפשרויות לנסות כשמודל לא מביא לנו תוצאות מספיק טובות. נקשר כל אפשרות למה היא בדרך כלל יכולה לעזור לנו לפתור:
- להשיג עוד תצפיות – יכול לעזור לפתור בעיות של שונות גבוהה. הסברנו למעלה למה.
- להוריד מאפיינים – יכול לעזור לפתור בעיות של שונות גבוהה. בהורדת מאפיינים אנחנו מפשטים את המודל, ונמנעים מהתאמת-יתר.
- להוסיף מאפיינים – יכול לעזור לפתור הטיה גבוהה. בהוספת מאפיינים אנחנו מדייקים את המודל ונמנעים מהתאמת-חסר.
- הוספת מאפיינים פולינומים ($x_1^2$ וכו') – יעזור לבעיית הטיה גבוהה, כמו שראינו בדוגמה (אנחנו מדייקים את המודל).
- הקטנת הלמדא של הרגולריזציה – יכולה לעזור להטיה גבוהה. שימו לב, כמו שאמרנו – בהקטנת למדא אנחנו שואפים לערכים המקוריים של ההיפותזה, ולכן נקבל הטיה נמוכה יותר.
- הגדלת הלמדא – יכולה לעזור במקרי שונות גבוהה. בהגדלת הלמדא אנחנו הופכים את ההיפותזה ליותר "כללית", ולכן פחות מדויקת ועם שונות נמוכה יותר. זכרו שמטרת הרגולריזציה היא בהגדרה להימנע מהתאמת-יתר, שזוהי השונות הגבוהה.
הדבר נכון גם לרשתות ניורונים – רשת קטנה יחסית של נוירנים תכיל פחות פרמטרים, ואמנם תהיה יותר זולה לחישוב אבל גם יותר מועדת להתאמת-חסר (עלולות לא להיות מספיק יחידות כדי שהרשת תבין את כל הקשרים ולכן תייצר תוצאה יותר כללית). רשת גדולה יחסית תהיה עם יותר פרמטרים, יותר יקרה לחישוב ומועדת להתאמת-יתר. עם זאת, אנדרו מציין שעדיף בד"כ ללכת על רשת נוירנים גדולה יותר ולאזן אותה עם רגולריזציה מאשר ללכת על רשת קטנה שלא תוכל בהכרח להבין את כל הקשרים הרצויים.
עד כאן שבוע 6 א', ועכשיו ל שבוע 6 ב'
הערות, טענות, מענות? כתבו לנו בתגובות 😉

