קורס למידת מכונה – שבוע 7 א': מכונת וקטורים תומכים (SVM)

רוצים להיות מעודכנים בכל מה שעולה ולא לפספס שום דבר? הרשמו למינוי למייל: (שימו לב - אם נרשמתם ל"הכל", לא צריך לסמן גם את השאר - אתם סתם תקבלו מיילים כפולים)

שם*

אימייל*

Lists*

הכל

בינה מלאכותית וML

שבוע 7 א'

הפוסט הזה הוא החלק הראשון של השבוע השביעי. אם פספסתם או סתם לא זוכרים, לחצו כאן כדי לעבור לשבוע 6א' או כאן כדי לעבור לשבוע 6ב'.

הערה – אם אתם גולשים מהנייד, חלק מהנוסחאות עלולות "להימרח" לצדדים. סובבו את המכשיר לרוחב אם זה קורה.

כמו בשבוע הקודם, גם הפעם החלטנו לחלק את החומר לשני חלקים כדי שיהיה נוח יותר לקרוא.

מכונת וקטורים תומכים Support Vector Machines (SVM)

הערה: אם אתם רוצים להבין את החומר השבוע עד הסוף, יעזור לזכור טוב את כל מה שכתבנו על הפונקציה הלוגיסטית ב שבוע 3. אני לא מבטיח שאני אחזור פה על הכל.

עד עכשיו יצא לנו לגעת בכמה אלגוריתמים מעניינים וחשובים בלמידה מודרכת. לרוב, לא בהכרח שמה שהכי ישנה בעולם הלמידה המודרכת זה איזה אלגוריתם תבחרו, אלא היכולות שלכם בביצוע שלהם – כמו איזה מאפיינים לקחת, בחירת הפרמטרים ועוד. עם זאת, ישנו אלגוריתם אחד נוסף שנחשב מאוד חזק ופופולרי גם בתעשייה וגם באקדמיה, שנקרא מכונת וקטורים תומכים (SVM, ראו כותרת). בהשוואה לרגרסיה לוגיסטית ולרשת נוירונים, היתרון שלו נעוץ בכך שהוא לפעמים נותן פתרון נקי ועוצמתי יותר ללמידה של היפותזות לא ליניאריות. האלגוריתם וכל מה שמאחוריו יהיו הנושא שלנו השבוע הזה.

כדי להתחיל להבין אותו, נחזור לרגרסיה לוגיסטית – שם, אמרנו שפונקציית ההיפותזה שלנו היא הסיגמואיד – $h_\theta(x) = \frac{1}{1+e^{-\theta^T x}}$, ורצינו שעבור תצפיות ש $y=1$ גם ההיפותזה תהיה גדולה ממש מ0 וקרובה ל1. ניזכר בפונקציית העלות שהגדרנו לה (לתצפית בודדת):

$$ J(\theta) = -y\,\log(\frac{1}{1+e^{-\theta^T x}}) –(1-y)\,\log(1 – \frac{1}{1+e^{-\theta^T x}})$$

למי ששכח, את הפונקציה הזו הרכבנו מחיבור של שני חלקים –$y=1$ ו$y=0$ (החלק השמאלי והימני, בהתאמה. אם תציבו 1 או 0 תיראו שכל אחד משאיר רק צד אחד של הנוסחה). לפני שנמשיך, נסמן $z = \theta^T x$. בעברית, z הוא מכפלת הפרמטרים שמצאנו בתצפית ספציפית, או במילים אחרות הפלט של האלגוריתם שלנו, אותו ברגרסיה לוגיסטית אנחנו מכניסים לפונקציית הסיגמואיד כדי לקבל סיווג לקבוצה מסוימת.

הסיגמואיד היא אחלה פונקציה, אבל בלי להעליב, יש לה איזה עניין קטן שכדאי לשים לב אליו:

אם נתסכל על הגרף של הסיגמואיד, נשים לב שהמעבר בין תצפית שתיחזה כחיובית לעומת שלילית הוא מאוד רגיש – ב0 מתהפך הקו. יוצא מכאן דבר מעניין: במצב בו z הוא ממש גדול או ממש קטן, נקבל דבר מעולה – הערך הוא מאוד ברור. מצד שני, כשz נמצא באחד מהערכים האמצעיים, ה"החלטיות" לא גבוהה מספיק, מה שגורם לכל תצפית כזו לתת תרומה גבוהה מאוד לפונקציית העלות J. ההבחנה הזו היא מה שעומד בבסיס ההבדל באלגוריתם מכונת וקטורים תומכים לעומת הרגרסיה הלוגיסטית. המטרה היא לייצר אלגוריתם שייתן "מרווח" גדול יותר בין כל אפשרות סיווג. המרווחים הם ה"וקטורים התומכים".

פונקציית העלות SVM Cost Function

לכן, ההחלטה הייתה לקחת את שני חלקי פונקציית העלות, ולהציב במקומן שתי פונקציות אחרות שנקרא להן $cost_0$ ו $cost_1$ (0 ו1 בהתאם לערך של $y$), שתוצאתן היא שהz שלנו "מתכנסים" לתשובה בצורה יותר חדה וברורה בלי כל הפיתול באמצע:

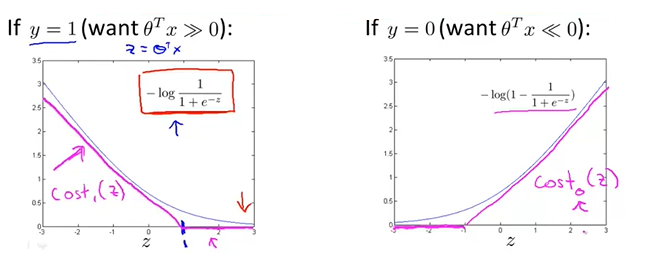
הגרף השמאלי הוא במקרה בו $y=1$, והימני כש$y=0$. הערך שלהם הוא התרומה של כל z לפונקציית העלות. הקווים הכחולים מסמנים את גרף הפונקציה הלוגיסטית לכל אחד מהמקרים – שימו לב לעיקול שלהן כשz הוא בערך "מתנדנד" (לדוגמה, בגרף השמאלי, כשz שווה ל0 או ערך שלילי, הערך שלו לJ דיי גבוה). לעומתם, הגרפים של SVM בורוד (אני יודע שקוראים לצבע מג'נטה אבל אני גבר) נותנים ערך יותר חד וברור – כשy שווה ל1, z יהיה 0 בנקודה 1. כשy מסווג ל0, z יהיה 0 רק במינוס 1. כך נוצר לנו המרווח שרצינו בין כל אפשרות.

אם בא לכם אקסטרה פורמליות, הנוסחה ל$cost_0$ היא $\max(0,1+z)$, ול$cost_1$ היא $\max(0,1-z)$ (בתמונה של הגרף זה לא הכי מדוייק מבחינת הערכים).

אם נחבר את שתי הפונקציות החדשות לפונקציית העלות של הרגרסיה הלוגיסטית, נקבל את זה:

$$\begin{align} \min_\theta & C \sum_{i=1}^m [y^{(i)} cost_1(\theta^Tx^{(i)}) + (1-y^{(i)}) cost_1(\theta^Tx^{(i)})] \\ & + \frac{1}{2} \sum_{i=1}^n \theta_j^2 \end{align}$$

לא להיבהל, זה ההסבר: היכן שהיו שני הלוגים של הרגרסיה הלוגיסטית, "שתלנו" את הפונקציות שלנו, $cost_0$ ו $cost_1$. כמו שאמרנו, זה ההבדל המרכזי בפונקציית העלות לעומת רגרסיה לוגיסטית. 2 ההבדלים הנוספים בנוסחה הם טכניים, נטו בשביל הנוחות:

הראשון הוא שהעלמנו את החילוק ב$m$ בשני הסיגמות בנוסחה. הסיבה שזה סבבה, היא כי כשאנחנו מחפשים מינימום של משהו (הסיגמות שלנו) ומכפילים\מחלקים אותו במספר קבוע (שזה $m$), מחיקה של המספר הקבוע עדיין תיתן אותה תוצאה (תחשבו על זה – אם היינו מנסים למצוא את המינימום של $x^2$, המינימום שהוא 0 לא היה משתנה גם אם היינו מכפילים את הנוסחה).

הדבר השני שעשינו הוא לשחק קצת עם פרמטר הרגולריזציה – הורדנו את $\lambda$ מהסיגמא השנייה, ובמקומו אנחנו מכפילים בפרמטר חדש בשם $C$ את הסיגמא הראשונה. מה שזה אומר לנו בתכלס, זה פשוט שהיחס הפוך – הרגולריזציה תמיד פועלת ב"100 אחוז", ואם אנחנו רוצים לתת יותר משקל לשגיאה שלנו (הסיגמא הראשונה), נכפיל אותה בC כדי שתשפיע יותר. בשורה התחתונה, $C = \frac{1}{\lambda}$ . C הוא ההופכי של מה שהיה הלמדא שלנו.

 מרווחי האלגוריתם Margins

אמרנו שהמטרה שלנו היא לייצר מרווחים גדולים יותר. כעת, אם עד עכשיו הספיק לנו ברגרסיה לוגיסטית לקבל ש $z\ge 0$ כדי ש$y=1$, עכשיו נצטרך $z\ge 1$, וכדי ש$y=0$ נצטרך ש$z \le -1$ במקום שיהיה קטן מ0. מעולה, אבל מה התוצאה של זה בפועל?

נניח שיש לנו שתי קבוצות שאפשר לחלק אותן ליניארית (Linearly separable, יעני שאפשר למתוח ביניהן קו ישר כשמפריד בין התצפיות של כל קבוצה). כל אחת אמנם נמצאת בצד אחר של הגרף, אבל איך נחליט איזה קו ובאיזה שיפוע כדאי למתוח ביניהם? הרי יש אינסוף אפשרויות.

כאן נכנס האלגוריתם – באופן אינטואיטיבי, הקו הכי הגיוני יהיה כזה שנמצא באיזשהו מרחק שווה בין שתי הקבוצות, וקשור לתצפיות שלהן באיזשהו מובן. דמיינו שולחן מלבני – אם הייתם צריכים לחלק אותו לשתיים (כמו שעושים בכיתה ב' כשמתעצבנים על חבר שלך לשולחן לדוגמה), כנראה שכולכם הייתם מותחים קו ישר בדיוק באמצע שלו. למרות שאפשר לחלק אותו לחצי גם לאורך או באלכסון, הבנתם שזו תהיה הדרך ש"מגדירה" הכי טוב כל חלק – השולחן מלבני ואנחנו עומדים מולו, לכן זה הכי הגיוני. על ההיגיון הזה נשען האלגוריתם.

אצלנו, אם 0 הוא האמצע, יצרנו כעת מרווח של 1 לכל צד. כתוצאה, הקו שיתקבל כהיפותזה הוא כזה שיש משני צדדיו עוד שני "קווים" (הווקטורים התומכים), שהמרחק ביניהם לכל קבוצה הוא המקסימלי האפשרי. המרחק הזה מכל קבוצה נקרא הרווח (margin). מסיבה זו לפעמים קוראים לאלגוריתם גם מסווג רווח רחב (Large margin classifier). ככה כל מה שדיברנו עליו נראה בתמונה:

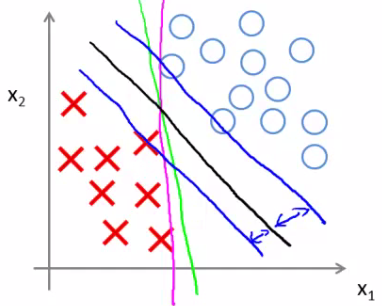
הקו הירוק והורוד הם אפשרויות להפרדה, הקו שחור מייצג את הקו (ההגיוני יותר) שהיינו מקבלים מהאלגוריתם, ושני הקווים הכחולים הם הווקטורים התומכים כביכול. ההפרש בין כל וקטור לשחור הוא המרווח.

גם במצב שיש לנו תצפיות חריגות (outliers) או קבוצות שלא ניתנות להפרדה ליניארית, האלגוריתם עדיין יכול למצוא קו איכותי והגיוני, פשוט צריך לשחק עם הרגולריזציה. זכרו שכאן הוא הפוך מלמדא – אם C קטן יש הרבה רגולריזציה, ואם הוא גדול יש מעט.

הסבר מתמטי נוסף

החלק הזה הוגדר כ"רשות" ודורש הבנה (טובה?) באלגברה ליניארית. אבל היי אתם כבר פה אז למה לא?

הסיבה שהאלגוריתם עובד כמו שראינו היא בגלל המשמעות שיש למרווחים שיצרנו. מבחינה אלגברית, כל תצפית היא למעשה וקטור. באופן דומה, גם ה$\theta$ שלנו היא וקטור מסוים. לכן, כשאנחנו מחשבים את ההיפותזה שלנו, $\theta^Tx^{(i)}$, אנחנו בעצם מבצעים מכפלה סקלרית (dot product) של התצפית על $\theta$. כדי לרענן את הזיכרון, מכפלה כזאת של ווקטור מסוים בחברו נותנת את ההיטל של אותו ווקטור על הווקטור השני כפול האורך (הכיוון זה יותר מדויק) של הוקטור השני. במקרה שלנו, זה אומר ש $\theta^T x^{(i)} = p^{(i)}\cdot \lVert \theta \rVert$, כש$p^{(i)}$ הוא ההיטל של התצפית $x^{(i)}$ על תטה מוכפל באורך של תטה.

עכשיו אפשר לכתוב את הכללים לסיווג ככה – נרצה ש$p^{(i)}\cdot \lVert \theta \rVert \ge 1$ אם $y^{(i)}=1$ ו$p^{(i)}\cdot \lVert \theta \rVert \le -1$ כש$y^{(i)}=0$.

עכשיו שימו לב לסיגמא השנייה (של הרגולריזציה) בביטוי שאנחנו מנסים לצמצם. אם נפתח אותו, נשים לב בעצם שאנחנו מנסים להביא למינימום את אותו האורך של $\theta$:

$\begin{align} \min \frac{1}{2}\sum_{j=1}^n \theta_j^2 & = \frac{1}{2} (\theta_1^2+..\theta_n^2)   = \frac{1}{2} (\sqrt{\theta_1^2+..\theta_n^2})^2 \\ & = \frac{1}{2} \lVert \theta \rVert \end{align}$

עכשיו נחבר את החלקים. כהקדמה, נציין שהווקטור $\theta$ תמיד יהיה אנכי לקו ההחלטה. אפשר להראות את זה אלגברית אבל פשוט תאמינו לי כרגע (כיוון שהנוסחה לקו ההחלטה היא $\theta^Tx+b = 0$, אפשר לראות את $x$ כווקטור בין כמה נקודות עליו ולכן האפשרות היחידה שהמשוואה תהיה שווה ל0 היא אם $\theta$ אורתוגונלי. הנה שמחים?):

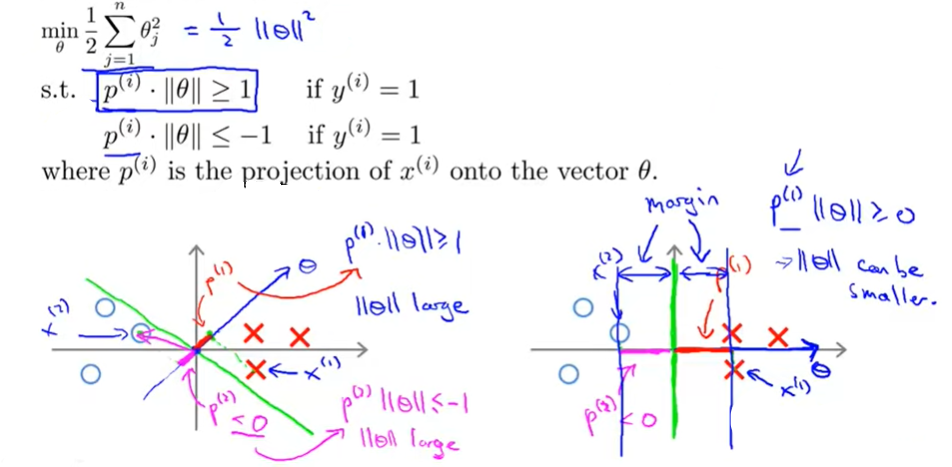
נסתכל על הגרף משמאל עם הקו הירוק העדין. ההיטלים (p) שיתקבלו מכל תצפית על $\theta$ יהיו מאוד קטנים (הקו החלטה עובר קרוב מאוד, תטה תהיה אנכית לו ותעבור קרוב יותר לתצפיות). לפי הכללים, כדי לקבל את הסיווג שאנחנו רוצים (גדול מ1 או קטן מ-1) נצטרך ש$\lVert \theta \rVert$ יהיה מאוד גדול כדי לפצות על זה – אבל כמו שניחשתם, זה לא אפשרי כיוון שבפונקציית העלות אנו מנסים להביא למינימום את אותו $\lVert \theta \rVert$ בדיוק!

לכן, הדרך שבה האלגוריתם ילך היא לצמצם את האורך כמה שניתן, וכתוצאה יתקבל הקו מימין. כיוון ש$\lVert \theta \rVert$ מינימלי, האפשרות היחידה שנשארת להיטלים של התצפיות שלנו על $\theta$ (יעני $p$) היא להיות כמה שיותר גדולים. התוצאה המתקבלת היא קו החלטה, שהמרחק המינימלי בינו לבין כל התצפיות מכל קבוצה הוא הגדול ביותר האפשרי. במילים אחרות, בכך שהאלגוריתם שואף להביא למינימום את אורך $\theta$, הוא מביא למקסימום את המרווחים של הווקטורים התומכים לכל קבוצה.

עד כאן שבוע 7א', יאללה ל שבוע 7ב' !

ספרו לנו מה אתם חושבים על החומר בתגובות