שבוע 9 א'
הפוסט הזה הוא החלק הראשון של השבוע התשיעי. אם פספסתם או סתם לא זוכרים, לחצו כאן כדי לעבור לשבוע 8א' ו שבוע 8ב'.
הערה – אם אתם גולשים מהנייד, חלק מהנוסחאות עלולות "להימרח" לצדדים. סובבו את המכשיר לרוחב אם זה קורה.
החומר של השבוע חולק לשני חלקים כדי שיהיה נוח יותר לקרוא.
גילוי חריגות Anomaly Detection
גילוי חריגות בא לענות על שאלה מאוד בסיסית במודלים שלנו – איך לזהות תצפיות "חריגות" מתוך סט הנתונים שלנו, ואיך להתייחס אליהם?
נניח שאתם נמצאים במפעל לייצור מנועים. כל מנוע יוצא מהפס ייצור קצת שונה – אחד רוטט יותר או פחות, מתחמם יותר או פחות וכן הלאה, כך שאין ערכים קבועים למאפייני המנוע, אבל כן אפשר לומר שיש טווחי ערכים שכל מנוע שנמצא בהם הוא עדיין סבבה. לעומת זאת, אם מנוע מתחמם הרבה יותר משאר המנועים או בעל כל ערך קיצוני אחר – ברור לנו שמדובר במנוע חריג שלא נוכל למכור ללקוח. המטרה שלנו תהיה לנסות לקלוט בזמן תצפיות חריגות – מנועים כאלו, ולהוריד אותם מפס הייצור או לשלוח אותם לאבחון.
כדי לזהות תצפית חריגה כזו, אנחנו נייצר דרך התצפיות פונקציית הסתברות $p(x)$, שתיתן לכל תצפית כלשהי את ההסתברות שהיינו מקבלים אותה. בהתאם, נקבע ערך שנסמן בתור $\epsilon$, שישמש בתור ה"רף" שלנו – אם ההסתברות של תצפית מסוימת היא מתחת לרף, נזהה אותה כחריגה. הדרך לבניית פונקציית הסתברות כזו ולזיהוי חריגים, טמונה בהבנה של איך כל מאפיין מתפלג. ברגע שנתחם כל משתנה עם ההתפלגות שלו, נוכל לזהות את התצפיות שסוטות מהממוצע. אחת ההתפלגויות שנעזר בהן כדי למדל את פונקציית ההסתברות שלנו תהיה ההתפלגות הנורמלית.
התפלגות נורמלית (גאוסיאנית) Normal (Gaussian) Distribution
מי שמכיר ושולט יכול לדלג קצת, אבל אפשר בכל מקרה לקרוא עדיין. אני אנסה להקיף את הנושא מאפס:
שמדברים על "התפלגות" של משתנה או מאפיין, הכוונה היא לדבר על ה"צורה" שבה הוא מופיע, ויותר ספציפית: איך הוא נע מבחינת הסתברות על מנעד הערכיים האפשריים שלו. יש משתנים שאם ניקח הרבה דוגמות שלהם, נראה שהסיכוי לקבל כל ערך הוא שווה (דמיינו פשוט קו ישר). יש כאלו שיש סיכוי הרבה יותר גבוה לקבל ערך גבוה מאשר ערך נמוך (כמו מגלשה מימין לשמאל), ועוד.
בענף הסטטיסטיקה, קיימות כמה התפלגויות מעניינות וחשובות, כאשר המוכרת והנפוצה מכולם היא ההתפלגות הנורמלית, בזכות ההימצאות הרבה שלה במציאות שלנו, ובזכות משפט חשוב בהסתברות שנקרא "משפט הגבול המרכזי", שהוא בקצרה קובע שתחת כמה תנאים, הרבה דגימות של משתנים מקריים (=רנדומלים) בלתי תלויים (אחד בשני) בסוף שואף להתפלג בהתפלגות הנורמלית. ניתן דוגמה:
בואו נחשוב רגע על המאפיין "גובה אנושי" – יש לו איזו "תבנית", או "פריסה": יש מספר אנשים נמוכים מאוד או גבוהים מאוד, אבל בסך הכל רוב הגבהים נמצאים קרוב מאוד לאיזה ממוצע מסוים. לכן ככל שאנחנו מרחיקים ימינה (גבוה יותר) או שמאלה (נמוך יותר), נמצא פחות ופחות אנשים עם גובה כזה. אם נדבר על הגובה במונחים של גרף, נקבל עקומה בצורה של "פעמון" – לאדם רנדומלי יש הרבה סיכוי לגבהים האמצעיים, וירידה כמו מגלשה בהתאם להתרחקות מהאמצע (שהוא ממוצע הגובה האנושי). הצורה הזו של ה"תבנית" היא שנקראת התפלגות נורמלית.
כדי לומר שx מתפלג בצורה נורמלית, נכתוב: $x^{(i)} \sim \mathcal{N}(\mu,\sigma^2)$, כשה~ מציין "מתפלג", N מציין Normal (יעני מתפלג נורמלית), וכמו שראינו עד עכשיו, האות $\mu$ היא הממוצע של המשתנה $x^{(i)}$, ו$\sigma^2$ זו השונות – ערך שמתייחס לסטייה מהמרכז.
ההתפלגות הנורמלית היא מאוד פשוטה. כדי למצוא את הממוצע והשונות של מאפיין מסוים שהחלטנו שהוא מתפלג נורמלית, נעשה מה שאנחנו מכירים עד עכשיו – הממוצע של ערכי המאפיין על כל התצפיות, והחישוב של השונות יהיה פשוט הממוצע של ההפרשים בין ערכי התצפיות לבין הממוצע (יעני לכל מאפיין נחשב $x – \mu$ ובסוף נחלק במספר התצפיות). אם יש לנו n מאפיינים וm תצפיות, החישובים למאפיין $j$ ייראו ככה:
לממוצע – $\mu_j = \frac{1}{m} \sum_{i=1}^m x_j^{(i)} $.
לשונות – $\sigma_j^2 = \frac{1}{m} \sum_{i=1}^m x_j^{(i)} – \mu_j $.
שימו לב שאנו עוברים על כל התצפיות, וסוכמים את הערכים של המאפיין הספציפי $x_j$.
בניית האלגוריתם
כמו תמיד, נניח שיש לנו $m$ תצפיות ו$n$ מאפיינים. נתחיל לבנות את $p(x)$, הפונקציה שלנו שמקבלת תצפית ומוציאה את ההסתברות שלה. כדי להתחיל לבנות כזו פונקציה, נצטרך לקבוע התפלגות לכל מאפיין שלנו, לכן, הפונקציה שאנחנו בונים בעצם תיראה כך:
\begin{align} p(x) &= p(x_1; \mu_1, \sigma_1^2) \cdots p(x_n; \mu_n, \sigma_n^2) \\ &= \prod_{i=1}^n p(x_i; \mu_i, \sigma_i^2) \\ &= \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma_i^2}} \exp\left(-\frac{(x_i – \mu_i)^2}{2\sigma_i^2}\right) \end{align}
כאשר כל $x_i$ הוא מאפיין, והערכים בתוך הסוגריים הם הממוצע והשונות הספציפיים להתפלגות שלו. ה$\prod$ הגדול הזה זה סתם סימן מוסכם שפשוט אומר שרשור כפל (כמו $\sum$, רק לכפל במקום חיבור). את הפונקציה הזו נשווה לערך $\epsilon$ שקבענו, וכך נבדיל בין חריג לתקין. השורה האחרונה שאתם רואים זו הנוסחה עצמה שאיתה נחשב את $p$. בסטטיסטיקה הפונקציה הזו נקראת פונקציית הצפיפות, ומה שאתם רואים זה הנוסחה של פונקציית הצפיפות של ההתפלגות הנורמלית. (למי שמכיר קצת הסתברות, בפירוק של $p(x)$ אנחנו למעשה מניחים שכל אחד מהמאפיינים הוא בלתי תלוי באחרים. למרות שגם אם חלק מהם כן אנדרו אומר שזה עדיין ייתן תוצאה)
עכשיו נעבוד בצורה הבאה: נקטלג מראש מתוך התצפיות שלנו את אלה שאנחנו יודעים שיצאו חריגים, נסמן עבורם $y=1$, ולתקינים $y=0$. בדרך זו הפכנו את הבעיה למין בעיה של למידה מודרכת, כאשר האלגוריתם לגילוי חריגות שלנו בעצם מנסה לחזות בהצלחה את התצפיות החריגות. כעת, נחלק את הדאטה שלנו ל3 – אימון, אימות ובדיקה כמו שאנחנו מכירים, אבל עם שינוי חשוב – סט האימון יכיל אך ורק תצפיות תקינות. את התצפיות שתייגנו כחריגות נחלק בין סט האימות לסט הבדיקה בלבד. הסיבה לכך היא עצם המטרה – פונקציית ההתפלגות (שניצור על סמך סט האימון) צריכה ללמוד את ההתפלגות של התצפיות הרגילות, כדי שהיא תוכל לזהות את החריגות. אם נכניס לה חריגות היא תיקח אותן בחשבון והמודל עלול להיפגע.
אז לפי שלבים:
- ניקח את המאפיינים שלנו, ונחשב לכל אחד את מאפייני ההתפלגות הנורמלית שלו, $\mu$ ו$\sigma^2$.
- נבנה את המודל עם חישוב הפונקציה $p(x)$ על התצפיות של סט האימון, כולן תצפיות "תקינות".
- נריץ על סט האימות\הבדיקה את הפונקציה ונחזה בהתאם למה שלמדנו:
\begin{align*} y &= \begin{cases} 1, & \text{if $p(x) < \epsilon$} \\ 0, & \text{if $p(x) \ge \epsilon$} \end{cases} \end{align*}
למי ששם לב, "חריגים" כשמם כן הם, ובכן, חריגים. סביר להניח שלא יהיו הרבה כאלה, ולכן אם ננסה להעריך את ביצועי האלגוריתם על ידי אם הוא "קלע" נכון, לא נקבל מדד מייצג מספיק. במקום זאת, אפשר להשתמש במדדים אחרים שלמדנו כמו הPrecision/Recall, $F_1 score$ וכולי כמו שראינו בשבוע 6.
בנוסף, בדומה לטכניקות שלמדנו, בהרצה על סט האימות ניתן למצוא את ה$\epsilon$ המושלם לנו – ננסה כמה ערכים ונראה עבור איזה ערך האלגוריתם שלנו מזהה את החריגות באופן הטוב ביותר.
שימוש באלגוריתם
בתכלס, אם אנחנו מסמנים איזה תצפיות תקינות ואיזה לא, עולה השאלה למה לא להשתמש באלגוריתם למידה מודרכת וזהו? אז התשובה היא שאפשר, אבל לא תמיד כדאי. ההבדל נעוץ בחלוקה של הנתונים שלנו – במקרים בהם יש לנו קצת מאוד דוגמות חיוביות (חריגות. $y=1$. נניח בין 0-50) והמון שליליות, יש קושי מהותי לכל אלגוריתם ללמוד איך אמורה להיראות דוגמה "חריגה" טיפוסית. בנוסף, כל תצפית חריגה עתידית יכולה להיראות שונה לגמרי ממה שיש לנו. במצבים אלו, שימוש באלגוריתם גילוי חריגות יכול להועיל לנו – הוא בנוי על תשתית הסתברותית שמסוגלת לבחור יותר "בפינצטה" את הדוגמות המעטות שחורגות מהשאר.
לעומת זאת, במקרים בהם יש לנו כמות גדולה ומספקת של דוגמות משתי הקבוצות, האלגוריתם מסוגל כבר לגבש "הרגשה" טובה יותר בנוגע לאיך אמורה להיראות תצפית חיובית או שלילית, וגם סביר שתצפיות עתידיות יהיו דומות למשהו שהוא כבר מכיר, לכן במקרים אלו נכון יהיה להשתמש באלגוריתם למידה מודרכת.
אם נשווה שימושים של התחומים בתעשייה, נראה ש:
גילוי חריגות: ייצור (כמו דוגמת המנועים שלנו), פיקוח והשגחה על שרתים (לא נופל סתם ככה), זיהוי הונאה (קיימים אינסוף דרכים שונות לביצוע הונאות מתוך סך הפעולות האפשריות בכל תחום. למרות שבמקרה וכן יש לכם כבר הרבה מידע בנוגע להונאות לפעמים הבעיה עוברת לתחום של "למידה מודרכת").
למידה מודרכת: סיווג ספאם\רגיל (גם פה אפשרי להתייחס לזה כגילוי חריגות, אבל בימינו יש לנו המון דוגמות מייל של ספאם), חיזוי מזג אוויר, זיהוי מחלות ועוד.
בחירת ועריכת מאפיינים
לפי אנדרו, למרות שהאלגוריתם יעבוד סבבה גם עם מאפיינים שלא באמת מתפלגים נורמלית, כדאי לשחק עם הערכים כדי להפוך את ההתפלגות לכזו שנראית יותר כמו התפלגות נורמלית (כי מה שלא הורג משפר תמודל). הדרך לבחון מהי העקומה של ההתפלגות של המשתנה שלכם היא להדפיס היסטוגרמה של הערכים (פעולה hist באוקטב. היסטוגרמה זה גרף שמציג שכיחות של ערכים, חפשו בגוגל), ואם היא לא נראית כמו בהתפלגות נורמלית ("פעמון"), לעשות טריק על אותו מאפיין כדי להסיט את הערכים שייראו דומה יותר. טריקים יכולים לעשות $\log(x+c)$ על המאפיין x (כש$c$ הוא 0 או קבוע כלשהו, שחקו איתו), או להעלות בחזקה קטנה מ1.
נקודה נוספת היא בחירת מאפיינים מומלצים לבעיה הזו, וכאן יש כמה דברים שכדאי לחשוב עליהם – א', אם יש לכם תצפית חריגה שהאלגוריתם לא זיהה כי היא קרובה לתצפיות "טובות", נסו להסתכל עליה ספציפית, ולחשוב על מאפיין מייחד שאפשר להוסיף לה שיבדיל אותה משאר התצפיות. ב', נסו לחשוב על מאפיינים שבמקרה שיש חריגה, הערך שלהם יקפוץ ויהיה קיצוני וכך יהיה קל להבדיל אותם, לדוגמה: אם המאפיינים שלי הם שימוש בזיכרון, עומס מעבד ותעבורה ברשת, ניצור מאפיין חדש שיהיה עומס המעבד לחלק לתעבורה. כעת, מצב בו הCPU נתקע ומשתגע (נגיד בלולאה אינסופית או בקריסה) בלי קשר לעומס בתעבורה יזוהה כחריגה.
התפלגות רב נורמלית Multivariate Normal (Gaussian) Distribution
(הרחבה, לא חובה)
קיימת הרחבה לאלגוריתם גילוי החריגות שמשתמש בהתפלגות אחרת – התפלגות רב-נורמלית. שימוש בהתפלגות הזו לפעמים מצליח לזהות חריגות שהאלגוריתם שלמדנו לא מצליח, עם זאת גם לו יש יתרונות וחסרונות. נתחיל מדוגמה: נניח שיש לנו שני מאפיינים, ותצפית חריגה אחת, כשכל אחד מהמאפיינים שלה נמצא יחסית קרוב לאמצע ההתפלגות, אבל בהסתכלות על שניהם ביחד היא רחוקה משאר התצפיות:
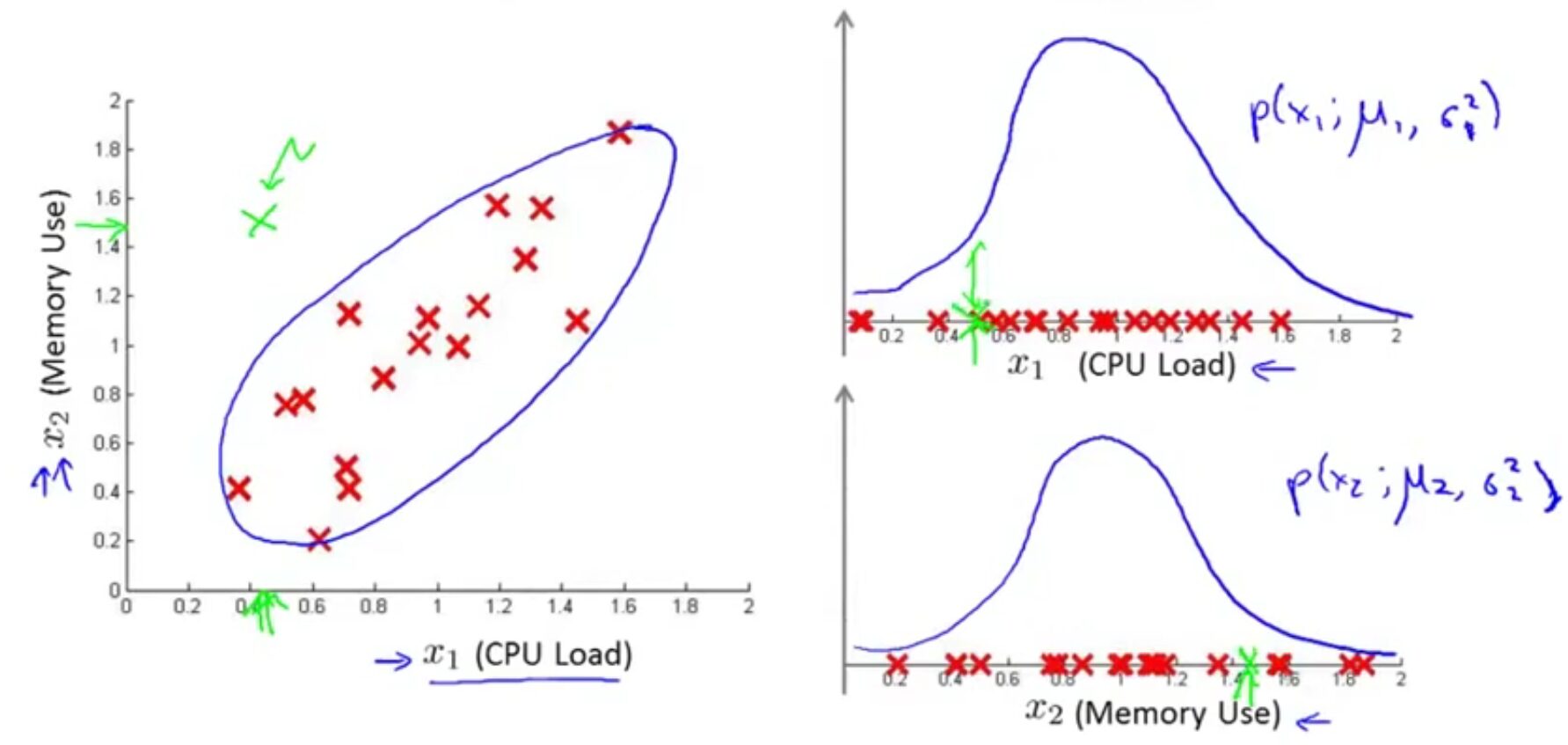
שימו לב שבגרף ההתפלגויות של שני המאפיינים בצד ימין, התצפית הירוקה נמצאת במקום סביר. לעומת זאת, כשאנחנו מדפיסים את הגרף בשני מימדים, ברור לנו שקיים איזשהו קשר בין שאר התצפיות לעומת התצפית הסוררת שלנו. אלגוריתם שמשתמש בהתפלגות נורמלית לא יצליח לזהות מקרה כזה כיוון שהוא מסתכל על כל מאפיין בפני עצמו, ולכן מבחינתו הסיכוי לקבל תצפית בכל כיוון שהוא מהמרכז הוא שווה, למרות שאנחנו רואים בבירור שזה לא המצב בדאטה שלנו.
לכן, נשתמש בהתפלגות רב-נורמלית – זו פשוט הכללה של ההתפלגות הנורמלית שלמדנו, אבל לכמה משתנים רב ממדיים במקום אחד נפרד. בהסתכלות כזו נוכל לקבל פונקציה שבנויה על חיבור של כמה מאפיינים, ולכן תוכל להתאים את עצמה יותר טוב ל"צורה" שמתקבלת משאר התצפיות. מבחינת נוסחאות, כמה דברים יישתנו. בפרט, במקום $\sigma^2$ נחשב כעת את מטריצת השונות המשותפת (מה שראינו עם הPCA), ו$p(x)$ לא תהיה פונקציה שמורכבת מהרבה פונקציות קטנות, אלא נוסחה אחת.
ככה זה בשלבים:
- ניקח את המאפיינים שלנו, ונחשב לכל המאפיינים ביחד את הפרמטרים של ההתפלגות הרב-נורמלית:
- $\mu = \frac {1}{m} \sum_{i=1}^m x^{(i)}$
- $\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)}-\mu) (x^{(i)}-\mu)^T$
- כעת, בהינתן תצפית חדשה $x$, נחשב את $p(x)$ כך:
$p(x) = \frac{1}{(2\pi)^{\frac{n}{2}}\det{\Sigma}^{\frac{1}{2}}} \exp ( – \frac{1}{2} (x – \mu)^T \Sigma^{-1}(x-\mu)) $
ונקבע אם זה חריג או לא בהתאם לערך שהתקבל מול $\epsilon$ כמו שראינו. אין מה להיבהל – כל הנוסחה של $p(x)$ זו פשוט נוסחת הצפיפות של ההתפלגות הרב-נורמלית, אפשר למצוא את זה בגוגל. למעשה, התפלגות נורמלית היא מקרה ספציפי של התפלגות הרב-נורמלית בו ערכי המאפיינים מיושרים אחד מול השני (במצב כזה, המטריצה $\Sigma$ תהיה עם ערכים לאורך האלכסון שמתחיל ב(1,1) ועם אפס בכל שאר המטריצה).
השוואה בין המודלים וההתפלגויות:
המקורי (התפלגות נורמלית) – לא מסוגל לזהות קורלציות בין מאפיינים, לכן כדי שהאלגוריתם יגלה חריגות שקשורות לכמה מאפיינים, נצטרך ליצור קומבינציות שלהם בעצמנו (כמו ההוספה של המאפיין של הCPU). זול יותר לחישוב ("מתרחב" (scales) טוב יותר עבור n גדול, אפילו 10 או 100 אלף), ועובד גם אם מספר התצפיות $m$ קטן.
גרסת התפלגות רב-נורמלית – מזהה באופן אוטומטי קורלציות בין מאפיינים, אך לכן גם (בין היתר) יותר יקרה לחישוב (תסתכלו על המטריצה $\Sigma$, היא nxn(!), בנוסף לחישוב ההופכי שלה). בנוסף, בגלל החישוב הנצרך של $\Sigma^{-1}$, חייבים ש $m > n$ כי אחרת המטריצה לא הפיכה. אנדרו אומר שאם הלכתם על התפלגות רב נורמלית כדאי לא להתפשר רק ש$m$ יהיה יותר גדול בקצת אלא $m \ge 10n$ בערך.
לשימוש בהתפלגות רב-נורמלית יש את היתרון שלה בכך שהיא לא מוגבלת ומסוגלת לזהות קורלציות לבד, מצד שני הבונוס הזה עולה בהרבה חישובים כבדים. לכן, לפי אנדרו לרוב משתמשים במודל הרגיל ומוסיפים ידנית מאפיינים לפי הצורך.
עד כאן שבוע 9א' ! השבוע קצת ארוך, אבל מקווים שנהניתם 🙂

