שבוע 9 ב'
הפוסט הזה הוא החלק הראשון של השבוע התשיעי. אם פספסתם או סתם לא זוכרים, לחצו כאן כדי לעבור לשבוע 9א'
הערה – אם אתם גולשים מהנייד, חלק מהנוסחאות עלולות "להימרח" לצדדים. סובבו את המכשיר לרוחב אם זה קורה.
החומר של השבוע חולק לשני חלקים כדי שיהיה נוח יותר לקרוא.
מערכות המלצה Recommeder\Recommendation Systems
הנושא של "מערכת המלצה", דהיינו מערכת שאוספת מידע על משתמשים ונותנת להם המלצות זוכה ליותר פוקוס בתעשייה מאשר באקדמיה. למרות זאת, אנדרו מציין 2 סיבות שגרמו לו להחליט ללמד עליהן – הראשונה היא שהוא רצה להראות יישומים ב"עולם האמיתי" של למידת מכונה וזו דוגמה טובה, בנוסף לכך שכל שיפור בנושא הזה יכול לתת קפיצה קדימה גדולה. הסיבה השנייה היא שבניגוד למה שראינו עד עכשיו, כשהנושא של הבחירה של המאפיינים תופס נפח חשוב בבניית המודלים שלנו, מערכת המלצות היא דוגמה נגדית לסביבה שבה האלגוריתם לפעמים דווקא "בוחר" את המאפיינים הכדאיים בשבילך, ולכן היא מעניינת.
נבין את הבעיה והאלגוריתם דרך דוגמה: נניח שיש לנו אתר לסרטים, וכל משתמש צופה בסרטים ומדרג אותם. נסתכל על הטבלה הבאה, בה יש רשימת סרטים מול משתמשים והדירוג שהם נתנו:
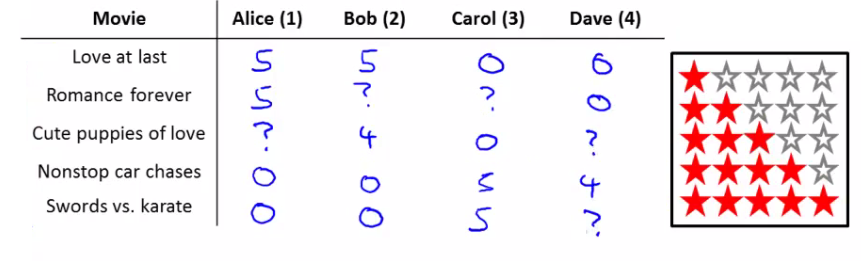
כל משתמש דירג סרטים, אך לא את כולם. אנחנו נרצה למצוא דרך לחזות את הערך שהמשתמשים היו מדרגים.
נסמן:
$n_u$ – מספר המשתמשים.
$n_m$ – מספר הסרטים.
$r(i,j)$ – האם המשתמש $j$ דירג את הסרט $i$. 1 אם כן, 0 אם לא (כמו פונקציה בוליאנית).
$y^{(i,j)}$ – הדירוג שהמשתמש $j$ נתן לסרט $i$ (שימו לב שזה מוגדר רק אם $r(i,j) = 1$).
קיימות שתי גישות לבניית אלגוריתם מערכת המלצות. נתחיל מהראשונה:
אלגוריתם מערכת המלצות מבוססת תוכן Content-based Recommender System
הבסיס הוא כזה – נכין לסרטים מספר מאפיינים שיתארו אותם (כמו אקשן, רומנטיקה, ועוד), ונקבע להם ערכים מתאימים לכל סרט (הסרטים משמשים כתצפית):
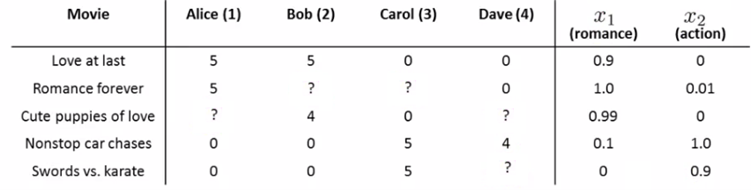
כעת, לכל משתמש $j$, נמצא פרמטרים $\theta_j$. בעזרתם, נכפיל את הפרמטרים בסרט שעליו אין לנו מידע ונמצא את הדירוג של אותו משתמש. בקטע יותר פורמלי, נסמן (בנוסף לקודמים):
$\theta^{(j)}$ – ווקטור הפרמטרים למשתמש $j$.
$x^{(i)}$ – ווקטור המאפיינים של הסרט $i$. גם פה אנחנו מוסיפים $x_0 = 1$.
עבור משתמש $j$ וסרט $i$, הדירוג החזוי יהיה $(\theta^{(j)})^T x^{(i)}$.
$m^{(j)}$ – מספר הסרטים שמשתמש $j$ דירג.
החישוב שנעשה כדי למצוא את הת'טות שלנו יהיה מינימיזציה של פונקציית העלות של ההפרש הממוצע בריבוע (MSE, בדיוק כמו ברגרסיה ליניארית) עם הוספת רגולריזציה לפי הצורך. לכל משתמש $j$, נעבור על הסרטים שהוא דירג ונחשב:
$\min_{\theta^{(j)}} \frac{1}{2} \sum_{i:r(i,j)=1} ((\theta^{(j)})^T x^{(i)} – y^{(i,j)})^2 + \frac{\lambda}{2} \sum_{k=1}^n (\theta_k^{(j)})^2$
בשונה מMSE רגיל, אנדרו הכפיל ב$m^{(j)}$ והוריד אותו מהמשוואה המקורית. כעת אם נכליל לכל המשתמשים, נקבל:
$\min_{\theta^{(1)}… \theta^{(n_u)}} \frac{1}{2} \sum_{j=1}^{n_u} \sum_{i:r(i,j)=1} ((\theta^{(j)})^T x^{(i)} – y^{(i,j)})^2 + \frac{\lambda}{2} \sum_{j=1}^{n_u} \sum_{k=1}^n (\theta_k^{(j)})^2$
ובהתאם, שלבי האלגוריתם מורד הגרדיאנט להגעה למינימום יראו כך:
$\theta_k^{(j)} := \theta_k^{(j)} – \alpha \sum_{i:r(i,j)=1} ((\theta^{(j)})^T x^{(i)} – y^{(i,j)})\cdot x_k^{(i)} \text{ for k=0} $
$\theta_k^{(j)} := \theta_k^{(j)} – \alpha \sum_{i:r(i,j)=1} ((\theta^{(j)})^T x^{(i)} – y^{(i,j)})\cdot x_k^{(i)} +\lambda \theta_k^{(j)}) \text{ for k$\neq$ 0}$
בדיוק כמו במה שראינו כבר, השורה הראשונה היא ל$x_0$ והשנייה זה לשאר.
לסיכום, השיטה המבוססת-תוכן נקראת כך כי היא מסתמכת על התוכן של התצפיות שלנו כשהיא באה לתת המלצות – הפכנו כל סרט ל"תצפית" עם מאפיינים, מצאנו $\theta$ לייצוג של כל משתמש, והפעלנו אותם על התצפיות כדי לקבל חיזוי לדירוגים השונים. עם זאת, מובן שלמצוא או להניח שיש לנו סט מאפיינים שיתאר את התצפיות זה לא קל (מי אמר שהערכים שנתנו לכל סרט באמת נכונים?), ולכן נעבור לשיטה שלא מניחה שיש לנו תשובות למאפיינים כאלו. היא נקראת
אלגוריתם סינון שיתופי Collaborative-Filtering Algorithm
גישת הסינון השיתופי הולכת לכיוון ההפוך – במקום להניח שיש לנו מאפיינים ואת ערכיהם, ודרכם לחשב את ה$\theta$ השונות ולהתחיל לחזות, נעשה הפוך: נניח שנתונות לנו כל התטות $\theta^{(1)}…\theta^{(n_u)}$ (הפרמטרים של כל משתמש), וכעת דרכם נחזה את המאפיינים השונים. ההיגיון הוא כזה – אם יש לנו ביד את ההעדפות של כל משתמש, נוכל להשתמש בהחלטות האלו כדי להבין מניסיונם מה הערכים הנכונים לכל מאפיין בתצפית. לדוגמה, אם יש לנו שני משתמשים שאנחנו יודעים שהם מדרגים גבוה סרטי רומנטיקה, כשנראה סרט שהם דירגו גבוה נוכל להסיק שהוא מאותו הז'אנר.
למעשה, אפשר לראות את שתי הגישות כשתי תשובות אפשרויות לשאלה של הביצה והתרנגולת – מה נתון לנו קודם, העדפות המשתמשים או מאפייני התצפיות. הגישה המבוססת תוכן, אומרת שבהינתן התצפיות נשערך את $\theta$, בעוד שהסינון השיתופי אומר שה$\theta$ נתונות ונשערך את התצפיות $x^{(i)}$
מטרת האלגוריתם תהיה להביא למינימום את הנוסחה:
$\min_{x^{(1)},\ldots,x^{(n_m)}} \frac{1}{2} \sum_{i=1}^{n_m} \sum_{j:r(i,j)=1} ((\theta^{(j)})^T x^{(i)} – y^{(i,j)})^2 + \frac{\lambda}{2} \sum_{i=1}^{n_m} \sum_{k=1}^n (x_k^{(i)})^2$
שימו לב לדמיון ולשוני בנוסחה לעומת הנוסחה בגישה הקודמת, ניגע בזה עוד רגע.
הגישה הזו נקראת סינון שיתופי כיוון שהיא בונה על ההבחנה שכשמריצים אלגוריתם כזה על מאגר גדול של מידע, כל משתמש למעשה "עוזר" בצורה שיתופית לאלגוריתם (ולשאר המשתמשים) לקבל הבנה טובה יותר של ערכי המאפיינים של כל פריט. בכל דירוג שמשתמש חדש מוסיף הוא תורם לחידוד הערכים של כל סרט ולשיפור ההמלצות של האלגוריתם. עכשיו נפתח את השיטה הזו קצת יותר בעזרת טכניקה שתעזור לנו להוריד זמן חישוב.
כיוון שאין לנו את ה$\theta$ באמת, הדרך שבה נתחיל לעשות את זה במציאות תהיה פשוט לתת להם ערכים רנדומליים, משם להשתמש בנוסחה למעלה כדי למצוא את כל ה$x$-ים, ואז להשתמש בנוסחת המינימיזציה ההפוכה (שראינו בגישה השנייה) כדי לשפר את $\theta$, וכן הלאה עד שנתכנס. פתרון כזה אמנם עובד, אבל אפשר לעשות אותו יותר טוב – אם נחזור לשתי הנוסחאות, נשים לב שהסיגמא המרכזית בכל אחת מהן בעצם סוכמת את אותו דבר – פעם אחת היא עוברת על התצפיות ופעם אחת על התטות, ולשניהם מחשבת את ההפרש בין התוצאה שקיבלנו לבין ה$y$ המתאים. אם כך, אפשר פשוט לייעל את התהליך ולחשב את שני השלבים (מינימום של $\theta$ ושל $x$) במקביל. נחבר את הנוסחאות ונקבל:
$J(x^{(1)},\ldots,x^{(n_m)},\theta^{(1)},\ldots,\theta^{(n_u)}) =$$\frac{1}{2} \sum_{(i,j):r(i,j)=1} ((\theta^{(j)})^T x^{(i)} – y^{(i,j)})^2 + \frac{\lambda}{2} \sum_{i=1}^{n_m} \sum_{k=1}^n (x_k^{(i)})^2$$+ \frac{\lambda}{2} \sum_{j=1}^{n_u} \sum_{k=1}^n (\theta_k^{(j)})^2$
הסיגמא הראשונה פשוט עוברת על כל הדירוגים, ושני האחרות הן הרגולריזציה של התצפיות ושל התטות מהפונקציות הקודמות. כעת פשוט נביא את פונקציית העלות הזו למינימום. פורמלית:
$\min_{\substack{x^{(1)},\ldots,x^{(n_m)} \ \theta^{(1)},\ldots,\theta^{(n_u)}}} J(x^{(1)},\ldots,x^{(n_m)},\theta^{(1)},\ldots,\theta^{(n_u)})$
נקודה אחרונה – בגישה הזו אין לנו צורך לקבוע בעצמנו $x_0=1$, כיוון שעכשיו נתנו לאלגוריתם את הגמישות ללמוד את המאפיינים בעצמו ולקבוע את הערכים שלהם. אם האלגוריתם יראה שכדאי להכניס משתנה שיהיה שווה 1, הוא פשוט יעשה את זה. לסיכום הגישה, אלו השלבים של האלגוריתם:
- נאתחל את $ x^{(1)}..x^{(n_m)},\theta^{(1)}..\theta^{(n_u)}$ בערכים רנדומליים קטנים.
- נביא את $ J(x^{(1)}..x^{(n_m)},\theta^{(1)}..\theta^{(n_u)})$ למינימום דרך שימוש במורד הגרדיאנט (או אלגוריתם מינימיזציה אחר) לכל $x^{(i)}$ וכל $\theta^{(j)}$:
$x_k^{(i)} := x_k^{(i)} – \alpha \sum_{j:r(i,j)=1} ((\theta^{(j)})^T x^{(i)} – y^{(i,j)})\cdot \theta_k^{(j)} +\lambda x_k^{(i)})$
$\theta_k^{(j)} := \theta_k^{(j)} – \alpha \sum_{i:r(i,j)=1} ((\theta^{(j)})^T x^{(i)} – y^{(i,j)})\cdot x_k^{(i)} +\lambda \theta_k^{(j)})$
- עבור משתמש עם הפרמטרים $\theta^{(j)}$ ותצפית (סרט) עם המאפיינים (שלמדנו) $x{(i)}$, נחשב: $(\theta^{(j)})^T x^{(i)}$
וקטוריזציה ומציאת פריטים דומים
כדי לחשב את כל ה$Y$ שלנו, פשוט נחשב $X \Theta^T$ , כאשר $X$ זו המטריצה של המאפיינים של כל התצפיות (סרטים), ו$\Theta$ היא מטריצה דומה של ה$\theta$ של כל המשתמשים. הוקטוריזציה הזו נקראת גם Low Rank Matrix Factorization (low rank זה פשוט מונח מתמטי שקשור למטריצות ובעיות מינימום).
אנחנו יודעים שאחרי שהאלגוריתם מסיים, נקבל לכל פריט (תצפית\סרט) $i$ וקטור מאפיינים תואם $x^{(i)}$. לכן, נוכל פשוט להסתכל על כל אחד מהפריטים כאל נקודה במרחב, ופשוט למדוד את המרחק ביניהם – אם נראה פריטים שהמרחק ביניהם הוא קטן, זה יהיה סימן טוב לכך שהם דומים באיזשהו מובן. החישוב יתבצע כמו שכבר ראינו בעבר למרחק בין נקודות: $\lVert x^{(i)} – x^{(j)} \rVert$. אם לדוגמה משתמש מסתכל כרגע על הסרט "שכחו אותי בבית", נחפש לו עוד 5 סרטים שהמרחק ביניהם אליו הוא מינימלי ונציג אותם לאותו המשתמש.
נרמול על פי ממוצע
הנקודה האחרונה לגבי המימוש של אלגוריתם הסינון השיתופי היא לנרמל את הערכים על פי ממוצע, מה שיכול לשפר קצת את הביצועים. את הסיבה שזה יכול לעזור ניתן להבין מהדוגמה הבאה:
נניח שלדוגמה שלנו עם הסרטים נוסיף משתמש חמישי שעדיין לא דירג אף סרט. נסתכל על פונקציית העלות שלנו – כיוון שהוא לא דירג אף סרט, הסיגמא המרכזית שמחשבת את ההפרש לא רלוונטית, הסיגמא השנייה (של ה$x_k^{(i)}$ רלוונטית רק לסרטים עצמם ולכן נשארנו רק עם הסיגמא השלישית, שמחשבת רגולריזציה ל$\theta$. עם זאת, בגלל שהמטרה של הפונקציה היא להביא את הערכים למינימום, האלגוריתם ייתן ל$\theta^{(5)}$ של אותו משתמש חדש ערכים של 0 בכל השדות.
הדבר הזה יגרום לנו לקבל משתמש חמוץ – אם נרצה לחזות עבורו דירוג לכל אחד מהסרטים, נקבל כל הזמן אפס (כי אנחנו מכפילים את התטה שלו במאפייני הסרט). צופה שכל הזמן מדרג 0 לכל הסרטים שלנו הוא לא שימושי במיוחד (אלא אם הוא באמת הייטר ואז haters gonna hate). כדי להתגבר על זה, נרמל בצורה הבאה:
ניקח את מטריצת הדירוגים שלנו, $Y$, ונחשב מעתה לכל סרט $x^{(i)}$ את ממוצע הדירוגים שלו $\mu_i$, ונערוך את המטריצה כך שכל דירוג שקיבלנו יהיה פחות הממוצע – $y(i,j) – \mu_i$. נריץ כעת את האלגוריתם למציאת המאפיינים והתטות כרגיל. כזה יסתיים, נחזה את הדירוגים למשתמשים עם אותה נוסחה שהשתמשנו מקודם בתוספת של ממוצע הדירוגים של אותו סרט:
$y(i,j) = (\theta^{(j)})^T x^{(i)} + \mu_i$
הנרמול הזה יפתור לנו את הבעיה – כעת, כל משתמש שכבר דירג במילא יקבל את אותו ערך (כי בהתחלה החסרנו ואז החזרנו לערך את הממוצע), אבל משתמשים חדשים שהתוצאה של החלק הראשון תהיה שווה להם ל0, יקבלו פשוט דירוג ממוצע של שאר המשתמשים. נרמול כזה יכול לעזור לנו בהמשך לדוגמה להציע למשתמשים חדשים סרטים פופולריים שמשתמשים אחרים דירגו כציון גבוה. למי שתהה – אין צורך גם לחלק את ערכי הדירוגים בשונות (או בטווח הדירוגים) כמו שעשינו כשעשינו נרמול למאפיינים של רגרסיה ליניארית למשל, כיוון שבמקרה של מערכת המלצות אנו יודעים להשוות בין דירוגים שונים (2 כוכבים גדול ב1 מכוכב אחד וכן הלאה), ולכן הם כבר על אותו סולם ערכים.
עד כאן לשבוע ה9 ! היה קצת ארוך (קצת..) אבל אנחנו מאמינים בכם. כדי להמשיך לשבוע ה10, לחצו כאן.
הערות או תלונות (גם על האורך) ניתן לכתוב לנו בתגובות 🙂

