שבוע 6 ב'
הפוסט הזה הוא החלק השני של השבוע השישי. אם פספסתם או סתם לא זוכרים, לחצו כאן כדי לעבור לשבוע 6א'.
הערה – אם אתם גולשים מהנייד, חלק מהנוסחאות עלולות "להימרח" לצדדים. סובבו את המכשיר לרוחב אם זה קורה.
תכנון מערכת למידת מכונה Machine Learning System Design
בואו נזכר בדוגמה על בניית אלגוריתם סיווג לזיהוי ספאם במייל. נניח שהחלטנו לבחור כמאפיינים כמות של מילים נפוצות באנגלית, ונסמן לכל מייל מסט האימון שלנו איזה מילים מופיעות בו. אימנו את המודל, וקיבלנו תוצאה. איך אפשר לשפר את המודל? יש שיגידו לאסוף עוד דאטה, יש שיחשבו על מאפיינים יותר מתוחכמים כמו להוסיף מאפיין לשורה או לכתובת המייל השולחת, או זיהוי שגיאות כתיב ועוד.
במקום לקום בוקר אחד וללכת עם "תחושת בטן" לגבי מה אפשר לשפר ולהיתקע על זה כמה ימים או חודשים, נרצה למצוא צורה שיטתית יותר להבין איזה שיפורים כדאי לנו להכניס למודל, ולכן נעבור לדבר עכשיו על –
ניתוח טעויות Error analysis
המטרה שלנו היא לקבל "הרגשה" יותר קונקרטית לגבי מה עשוי לעזור ומה לא. העניין הוא, שמובן שבלי עובדות מוצקות או גרפי מידע שונים יהיה לנו קשה להגיע להחלטה כזו. לכן, מטרה ראשונית מומלצת תהיה להשיג אותם כמה שיותר מהר. הנה דוגמה לגישה מומלצת, שלב אחרי שלב:
- תתחילו עם אלגוריתם פשוט שתוכלו ליישם ולהריץ מהר, ובדקו אותו על סט האימות שלכם. לא חשוב מאוד כרגע אם הוא קצת מבולגן או מלוכלך.
- תדפיסו עקומות למידה ממה שיש לכם, כדי להחליט אם עוד תצפיות, מאפיינים וכו' עשויים לעזור. (בין היתר עם כל מה שלמדנו עד עכשיו)
- ניתוח הטעויות – בדיקה באופן ידני של התצפיות (בסט האימות) שהאלגוריתם שלכם טעה בחיזוי שלהם. אם מדברים על זיהוי ספאם, הסתכלו על המיילים שהאלגוריתם סיווג לא נכון וחשבו האם יש איזה דפוס (pattern) חוזר על עצמו או כל טרנד אחר במיילים האלו, שאולי בגללם האלגוריתם טעה.
לדוגמה, נניח שמתוך 500 תצפיות של מיילים בסט האימות, טעינו ב100 (שבטעות סווגו כ"מייל רגיל" למרות שהם ספאם). כשנסתכל על המיילים, נוכל לחלק אותם לקטגוריות – זיוף, "זכיה פתאומית", גניבת סיסמאות ועוד. נוכל לחשוב על רמזים כמו שהזכרנו בפסקה הקודמה (שגיאות כתיב, שימוש בסימני קריאה\שאלה רבים). כל רמז כזה יכול ללמד אותנו במה האלגוריתם מתקשה ולשפר אותו בהמשך.
בנוסף, חשוב לזכור שכשעוסקים בניתוח הטעויות, צריך שתהיה לכם מדד להערכת הביצועים עם ערך מספרי – כמו אחוז השגיאה או א הדיוק של האלגוריתם. אחרי כל שינוי שלו אנחנו רוצים לדעת מה עבד ומה לא, ועד כמה.
קבוצות מוטות Skewed Classes
בדרך כלל, אפשר למצוא מדדים נוחים ומדויקים להערכת ביצועי האלגוריתם שלכם. במקרים אחרים, כמו לדוגמה במצב של קבוצות מוטות (skewed classes), זה עלול להיות קצת בעייתי:
נניח שאימנתם מודל רגרסיה לוגיסטית שקובע אם לחולה מסוים יש קורונה (טפו טפו) או לא: 1 אם הוא חולה, ו0 אם בריא, וגילינו שאחוז השגיאה בסט הבדיקה הוא 1% בלבד –את 99% הנותרים מהתצפיות הוא מזהה נכון. נשמע מדהים, נכון? לא כל כך בטוח.
אחרי זה הסתכלנו על הדאטה שלנו, וראינו שמתוך כל התצפיות, רק לחצי אחוז מהן יש את המחלה. במצב כזה, טעות של אחוז אחד כבר לא נשמעת מרשימה מידי. במקרה שלנו, אפילו אם ההיפותזה שלנו תהיה פונקציה "טיפשה" שקובעת לכל התצפיות $y=0$, נקבל אחוז שגיאה של 0.5% – יותר נמוך מהאלגוריתם!
שתי הקבוצות שלנו – של החולים והבריאים, מוטות מידי אחת מול השנייה, כך שהמדדים הרגילים שאנחנו מכירים לא באמת סימלו את איכות האלגוריתם. במקרים כאלו, נצטרך מדדים אחרים. וספציפית, נכיר שניים חדשים:
נכונות ואחזור Precision / Recall
הבעיה של סתם מדד דיוק (accuracy), כמו שהשתמשנו בו בדוגמה, היא שהמדד בודק כל תצפית רק בפני עצמה. הוא לא לוקח בחשבון את היחס בין התוצאה שהתקבלה מהאלגוריתם, ל$y$ המקורי – האם אפשר להתייחס לכל טעות סיווג, כמו 0 במקום 1, או 1 במקום 0, כאותה טעות? האם כל תשובה חיובית שקיבלתי היא באמת רלוונטית?
נסתכל על הדוגמה שלנו (עם 2 הקבוצות המוטות – חולה או לא), ונסביר:
לכל סיווג, יש שתי אפשרויות: או שהאדם היה חיובי או שלילי, 0 או 1 (positive and negative). על כל אפשרות כזו, יש עוד שתי תוצאות אפשריות לאלגוריתם – לצדוק ולטעות, במילים אחרות לומר אמת או שקר (true and false). לכן, גם כשהאלגוריתם שוגה בחיזוי – הוא יכול לטעות בשתי דרכים: הוא יכול לומר למי שחולה שהוא לא, והוא יכול לומר למי שאינו חולה שהוא כן. בסך הכל, נקבל 4 אפשרויות:
- חיובי אמיתי (true positive) :התצפית חיובית, והחיזוי (של האלגוריתם) חיובי – האלגוריתם צדק.
- שלילי אמיתי (true negative): התצפית שלילית, וגם החיזוי שלילי – האלגוריתם צדק.
- חיובי מזויף (false positive): התצפית שלילית, אבל החיזוי חיובי – האלגוריתם זייף.
- שלילי מזויף (false negative): התצפית חיובית, אבל החיזוי שלילי – האלגוריתם זייף.
כל אחת מהתצפיות של אלגוריתם הלמידה שלנו תיכנס לאחת מהאפשרויות האלו. בטבלה, זה ייראה כך:
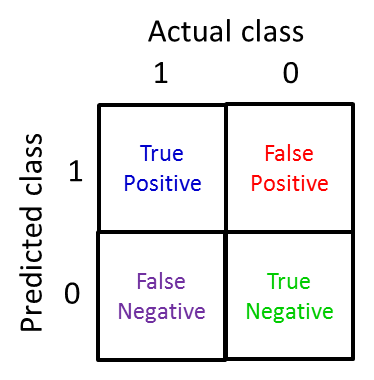
ההבחנה החשובה הזו ביחס בין הy הקיים להיפתוזה שלנו, מאפשרת לנו לחלק את הערכת האלגוריתם שלנו לשני מדדים: הנכונות (Precision), והאחזור (Recall, לפעמים נקרא גם רגישות, Sensitivity):
מדד הנכונות (אפשר אולי לתרגם גם "דייקנות"), שואל את השאלה הבאה – כמה תצפיות מתוך אלו שזוהו כחיוביות, באמת רלוונטיות לי? (זאת אומרת, כמה מהן היו חיוביות על אמת גם במקור?). כנוסחה, היא מוגדרת כך:
$$ \begin{align} Precision & = \frac {\text{True positives}}{\text{all predicted as positives}} \\ & = \frac {\text{true positives}} {\text{true positives + false positives}}\end{align}$$
בטבלה שבתמונה, זה החילוק של הכחול בכחול ביחד עם האדום (השורה הראשונה). המדד הזה מאפשר לנו "לברור את הפסולת" ולהבין כמה מתוך החיובים שקיבלנו אכן רלוונטיים לנו.
לעומתו, מדד האחזור (או "היזכרות" או "רגישות"), שואל שאלה אחרת – כמה תצפיות, מתוך אלו שהן רלוונטיות בשבילנו, האלגוריתם הצליח להחזיר? (זאת אומרת, מתוך סך התצפיות המקוריות שהן חיוביות, כמה מהן האלגוריתם זיהה וכמה לא?). כנוסחה, היא מוגדרת כך:
$$ \begin{align} Recall & = \frac {\text{True positives}}{\text{the real positives}} \\ & = \frac {\text{true positives}} {\text{true positives + false negative}}\end{align}$$
בטבלה שבתמונה, זה החילוק של הכחול בכחול ביחד עם הסגול (הטור הראשון). המדד הזה מאפשר לנו להבין כמה מתוך כל התצפיות הרלוונטיות שאנחנו כבר מכירים, האלגוריתם באמת ידע "לשים עליהם את האצבע".
שני המדדים נעים בטווח שבין 0 ל1, ובשניהם נשאף לקבל ערכים כמה שיותר גבוהים (משמע אין לנו שום טעויות בזיהוי). בשימוש במדדים אלו, בעיות של קבוצות מוטות לא יוכלו להתחמק מלקבל ציון גרוע, כיוון שאנחנו סופרים ממש את אחוז הטעות לפי אלו שהאלגוריתם היה צריך לזהות. אם נסתכל על הפונקציה הטיפשה שנותנת חיזוי של 0 לכל תצפית, נראה שכיוון שמספר החיוביים האמיתיים (true positives) יהיה 0 (כי הוא אמר על כולם שאין להם קורונה), ייצא שנקבל 0 בשני המדדים – מה שיכול לאותת לנו שהפונקציה הזו היא אינה כזו טובה.
האיזון בין המדדים (Trade-off)
נקודה נוספת שיש לשים אליה לב, היא הפשרה שלפעמים צריך לעשות בין שני המדדים האלו – נחשוב על $h_\theta(x)$ של הדוגמה שלנו. כשלמדנו על רגרסיה לוגיסטית ועל הסיגמואיד, קבענו את 0.5 להיות הסף (threshold) שקובע לנו לאיזו קבוצה לסווג כל תצפית. כש $h_\theta(x)>0.5$, נחזה 1, וכן להפך. לסף הזה יש משמעות:
נניח שכיוון שראינו שלבשר למישהו שהוא חולה קורונה זו בשורה קשה, החלטנו לחזות $y=1$ רק כשאנחנו מאוד בטוחים שזה באמת המצב. לכן העלנו את הסף לאיזור ה0.7 או אפילו 0.9. כתוצאה מכך, לרוב נקבל מדד נכונות מאוד גבוה – כיוון שהגבול יותר גבוה, רק תצפיות יותר מובהקות ייקבלו חיזוי חיובי, ופחות ייכנסו בטעות. מצד שני, הורדנו את מדד האחזור – כי אנחנו כנראה נשאיר יותר תצפיות חיוביות אמיתיות בחוץ.
במקרה הפוך, נניח שאנחנו מפחדים מאוד לפספס מקרה של קורונה. עכשיו אנחנו נעדיף דווקא להוריד את הסף (נניח ל0.3), ונראה שנקבל מדדים הפוכים – כן שיפרנו את מדד האחזור (כי יותר תצפיות חיוביות אמיתיות נחזו כחיוביות), אבל הורדנו את הנכונות (הכנסנו עוד ועוד מקרים וכנראה חלקם הם שליליים בכלל).
מטבע הדברים קיים קשר (לא בהכרח ליניארי, תלוי במודל שלכם) בין שני המדדים, ולכן חשוב להבין את האיזון שלפעמים צריך למצוא ביניהם כדי לקבל את התוצאה הרצויה. נקודה נוספת אחרונה בנוגע לשני המדדים היא איך ניתן להשוות ביניהם לכל אלגוריתם שהרצנו – השוואה של המדדים הישנים היא פשוטה יותר – או שזה גדול או שזה קטן יותר. איך משווים שניים לשניים? לחשב את הממוצע ולהשוות לא תמיד יעבוד (נסו לחשוב על הדוגמה של הפונקציה הטיפשה), לעומת זאת, יש הרבה מדדים אחרים.
המדד הנפוץ להשוואת מדדי אחזור ונכונות של אלגוריתמים נקרא $F_1 Score$, וזו הנוסחה שלו:
$$F_1 Score = 2 \frac{P \cdot R}{P+R}$$
כשP וR זה Precision וRecall, בהתאמה. המדד הזה מאפשר לשאוף לציון של 1 (הכי גבוה) במקרה ששני המדדים גבוהים, ו-0 כשהם נמוכים, מה שעוזר לשקלל אותם ביחד.
שימוש בהרבה תצפיות Large Data Sets
מאמר של שני חוקרים בשם בנקו ובריל שנערך ב2001, מצא ש4 אלגוריתמים מגוונים שנבחרו להתאמן על אותה בעיה, השתפרו כולם באופן מונוטוני עם העלייה בכמות התצפיות שהם קיבלו. המחקר הזה ביחד עם דוגמות נוספות הביא אנשים לראות באיסוף עוד דאטה ותצפיות ככלי חשוב לשיפור ביצועי האלגוריתם, עד כדי שלפעמים אומרים שזה לא מי שיש לו את האלגוריתם הכי טוב שמנצח, אלא מי שיש לו הכי הרבה דאטה. אך חשוב להבין שהמנטרה הזו נשענת על הנחה אחת חשובה – שהמאפיינים של האלגוריתם באמת מסוגלים לחזות את $y$ באופן מדוייק:
לדוגמה, נניח שכתצפית קיבלנו את המשפט "דני הלך __ רוני לקנות שזיף" ומטרת המודל היא להשלים את המילה החסרה. ממה שאנחנו רואים, יש לנו משפט מלא, ולכן סביר שהאלגוריתם יחליט ש"עם" (ולא מילים דומות כמו אם, הם, ים) היא המתאימה. מצד שני, אם יש לנו מודל שמטרתו לחזות מחירי בתים, והמאפיין היחידי שיש לנו זה השטח במ"ר, כנראה שלא נגיע רחוק.
לכן, חשוב לוודא שיש לנו מאפיינים מספיק טובים לבעיה שאיתה אנו מתמודדים. בדיקה טובה כדי לדעת אם יש לנו מאפיינים כאלו היא פשוט לשאול מומחה (או את עצמנו בראש): בהינתן התצפית שעומדת לפניי, האם מומחה לתחום היה מצליח לחזות את y בבטחה? אם היינו מציגים את המשפט שלנו לכל דובר עברית, הוא היה עונה עליו בקלות (אני מקווה). אם היינו מציגים לסוכן נדל"ן מטר רבוע של בית ומבקשים ממנו לומר כמה הוא עולה, לא בטוח כל כך שהוא היה מצליח לתת תשובה איכותית.
כעת, זהו הרציונל: בהינתן מודל למידה עם הרבה פרמטרים איכותיים, כדאי לנו להוסיף הרבה דאטה. תראו את היופי: עם הרבה פרמטרים, נקבל $J_{train}(\theta)$ נמוך, או במילים אחרות הטיה נמוכה (low bias) – כי האלגוריתם מדייק מאוד על סט האימון. אם נוסיף לזה הרבה דאטה – אנחנו מורידים את הסיכוי של האלגוריתם להתאמת-יתר או שונות נמוכה, מה שאומר ש$J_{train}(\theta)$ יהיה קרוב ל$J_{test}(\theta)$ – כי יש לנו כל כך הרבה דוגמות שזה לא ישנה כבר על מה התאמנו.
עכשיו, אם $J_{train}$ נמוך, והוא פחות או יותר שווה ל$J_{test}$, זה מביא אותנו למסקנה אחת – גם $J_{test}$ יהיה נמוך. לסיכום – נשאל את עצמנו א. האם הפרמטרים שלי מספיק איכותיים בשביל הבעיה (או "האם מומחה היה עונה על זה נכון?), וב. האם אנחנו יכולים להוסיף עוד תצפיות.
סיימנו את שבוע 6! למעבר ל שבוע 7, לחצו כאן.
שאלות? הערות? כתבו לנו בתגובות:

